给定等轴测图形的斜视图为
三个边长为 2 厘米的立方体并排放置形成长方体的斜视图:三个边长为 2 厘米的立方体并排放置形成长方体的等轴测视图
已知:长方体的尺寸为 5 厘米、3 厘米和 2 厘米。要求:绘制该长方体的三个不同的等轴测视图。解答:尺寸为 5 厘米、3 厘米和 2 厘米的长方体如下所示:给定长方体的三个不同的等轴测视图如下
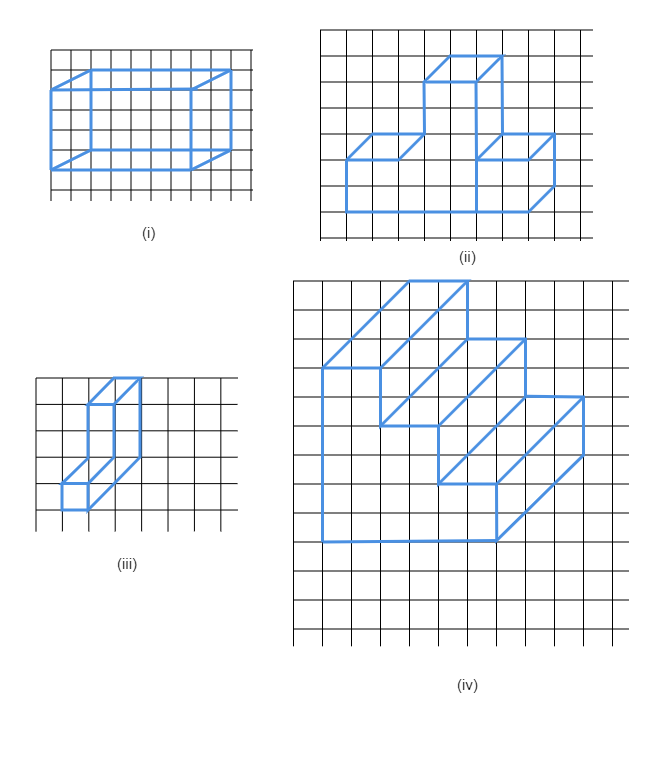
已知:给定不同形状的斜视图。要求:使用等轴测点图纸,为每个给定的形状绘制等轴测视图。解答:给定形状的等轴测视图如下:
已知:展开图和立体图形。要求:将展开图与相应的立体图形匹配。解答
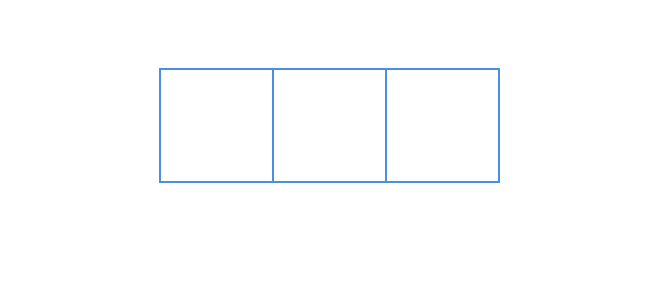
已知:立方体的未完成展开图。要求:用两种不同的方法完成立方体的展开图。解答:这里给出了立方体的三个面。我们知道立方体有 6 个面。所以我们必须再添加 3 个面才能以两种不同的方式制作一个完美的立方体。两种方法如下
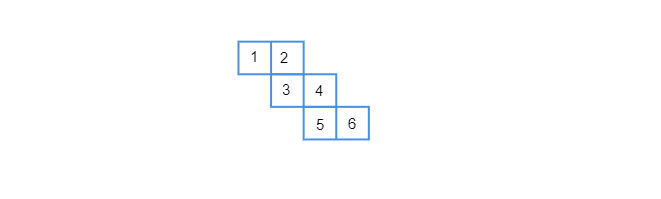
已知:一个展开图。要求:检查它是否可以作为骰子的展开图。解答:我们知道骰子是一个立方体,每个面上都有点。骰子的对面点数之和为 7。因此,给定的展开图不能作为骰子的展开图,因为它的对面点数之和不为 7。
已知:旋转角:$(i) 45^{\circ}$? $(ii) 17^{\circ}$?要求:找出是否我们可以有一个旋转对称阶数大于 1,其旋转角为:$(i) 45^{\circ}$? $(ii) 17^{\circ}$?解答:当一个物体绕一点沿特定方向旋转时,称为旋转对称,也称为径向对称。当一个形状被旋转,并且形状与原形状相同,则存在旋转对称。如果给定的角度是 $360^{\circ}$ 的因子,则该图形将具有大于 1 的旋转对称阶数。$(i) 45^{\circ}$ 是 $360^{\circ}$ 的因子,所以 ... 阅读更多
已知:绕中心旋转 $60^{\circ}$ 后,图形看起来与原始位置完全相同。要求:找到图形还会在什么其他角度发生这种情况。解答:如果图形在一个角度看起来像原始图形,那么它将在该角度的所有倍数上看起来像原始图形。因此,如果图形在旋转 $60^{\circ}$ 角时看起来与原始位置相同,则在旋转 $120^{\circ}$、$180^{\circ}$、$240^{\circ}$、$300^{\circ}$、$360^{\circ}$ 角时,它看起来也将相同,因为它们是它的倍数。
要求:命名既具有线对称性又具有大于 1 阶旋转对称性的四边形。解答:一条可以将图像折叠并使两半完全匹配的假想线,或者两幅图像都是彼此的复制品,被称为“对称线”。当一个物体绕中心点(旋转)旋转一定角度时,并且物体在这些角度看起来相同,则此处看到的对称性称为旋转对称性。对称阶数是物体看起来相同的位姿数 ... 阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP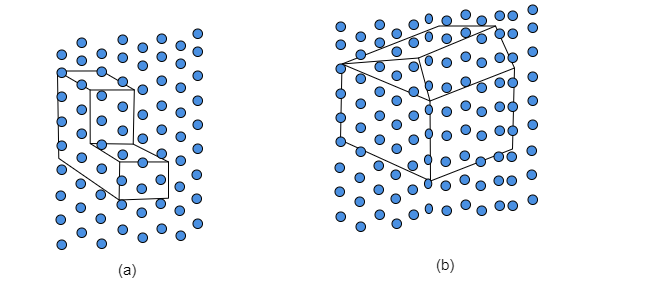 "\
"\
 "\
"\ "\
"\ "\
"\ "\
"\