数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学
"
题目：我们需要判断给定的陈述哪些是真哪些是假。解答：(i) 我们知道，无数条直线可以穿过一个点。因此，只有一个直线能穿过一个点的陈述是错误的。(ii) 我们知道，通过两个不同的点，只能画一条直线。因此，有无限多条直线能穿过两个不同的点的陈述是错误的。(iii) 我们知道，一条直线可以…… 阅读更多
题目：我们需要写出 $2x+9=0$ 作为方程的几何表示 (i)在一个变量中，(ii)在两个变量中。解答：(i) 我们知道，要绘制一个变量的线性方程的图形，我们只需要一个解。给定，$2x+9=0$这意味着，$2x=-9$$x=\frac{-9}{2}$$x=-4.5$因此，$x=-4.5$ 和 $y=0$ $2x+9=0$ 在一个变量中的几何表示是：(ii) 我们知道，要绘制两个变量线性方程的图形，我们需要至少两个解。$2x+9=0$ 可以写成 $2x+(0)y+9=0$ (两个变量)。为了找到方程 $2x+(0)y+9=0$ 的解，让我们将 $y=0, 1$ 和 $x=-4.5$ 代入… 阅读更多
题目：我们需要写出 $y=3$ 作为方程的几何表示 (i)在一个变量中，(ii)在两个变量中。解答：(i) 我们知道，要绘制一个变量的线性方程的图形，我们只需要一个解。给定，$y=3$这意味着，$x=0$ 和 $y=3$ $y=3$ 在一个变量中的几何表示是：(ii) 我们知道，要绘制两个变量线性方程的图形，我们至少需要两个解。$y=3$ 可以写成 $(0)x+y=3$ (两个变量)。为了找到方程 $(0)x+y=3$ 的解，让我们将 $x=0, 1$ 代入… 阅读更多
给定：将华氏度转换为摄氏度的线性方程是 $F=(\frac{9}{5})C+32$。题目：我们需要找到问题的解。解答：给定，$F=(\frac{9}{5})C+32$(i) 通过将摄氏度放在 x 轴上，华氏度放在 y 轴上，在图表上绘制线性方程。我们知道，要绘制两个变量线性方程的图形，我们需要至少两个解。为了找到方程 $F=(\frac{9}{5})C+32$ 的解。让我们将 $C=0$ 代入方程 $F=(\frac{9}{5})C+32$对于 $C=0$我们得到，$F=(\frac{9}{5})0+32$$F=32$对于 $C=-10$我们得到，$F=(\frac{9}{5})-10+32$$F=9(-2)+32$$F=-18+32$$F=14$因此，$(0, 32)$ 和 $(-10, 14)$ 是方程 $F=(\frac{9}{5})C+32$ 的两个解。因此，线性方程 $F=(\frac{9}{5})C+32$ 的图形在… 阅读更多
给定：雅米妮和法蒂玛是学校九年级学生，他们一起为帮助地震受害者向总理救济基金捐款 100 卢比。题目：我们需要写出一个满足给定数据的线性方程。解答：根据题意，设雅米妮的捐款为 $Rs.\ x$，法蒂玛的捐款为 $Rs.\ y$。因此，满足给定数据的线性方程是 $x+y=100$。我们知道，要绘制两个变量线性方程的图形，我们需要至少两个解。为了找到给定方程 $x+y=100$ 的解。让我们将 $x=0, 50, 100$ 代入… 阅读更多
给定：点 $(3, 4)$ 位于方程 $3y=ax+7$ 的图形上。题目：我们需要求 $a$ 的值。解答：根据题意，$(x, y)=(3, 4)$现在，将 $(x, y)=(3, 4)$ 代入方程，我们得到 $3(4)=a(3)+7$这意味着，$12=3a+7$$12-7=3a$$5=3a$$3a=5$$a=\frac{5}{3}$因此，$a$ 的值为 $\frac{5}{3}$。
已知：某城市出租车收费标准为：第一公里8卢比，之后每公里5卢比。要求：设行驶距离为x公里，总费用为y卢比，写出其线性方程并画出图像。解答：设行驶总距离为x公里。第一公里的费用 = 1 × 8 = 8卢比。之后距离的费用 = (x - 1) × 5卢比。根据题意，8 + (x - 1)5 = y⇒ 8 + 5x - 5 = y⇒ 5x - y + 3 = 0表示该信息的线性方程为5x - y + 3 = 0。我们知道，要绘制二元线性方程的图像…… 阅读更多
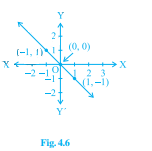
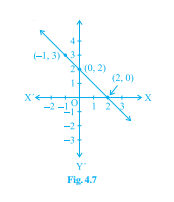
要求：找出图4.6和图4.7对应的方程。解答：对于图4.6，让我们将给定点代入选项中的每个方程。给定点应该满足图中所示方程。因此，(i) (-1, 1) y = x -1≠1 (ii) (-1, 1) x + y = 0 -1 + 1 = 0 0 + 0 = 0 1 - 1 = 0 因此，(-1, 1)和(1, -1)满足方程x + y = 0。(iii) (-1, 1) y = 2x 1 = 2(-1) 1≠-2 (iv) (-1, 1) 2 + 3y = 7x 2 + 3(1) = 7(-1) 2 + 3 = -7 5≠-7 因此，图4.6对应的方程是x + y = 0。对于图4.7，让我们将给定点代入选项中的每个方程…… 阅读更多
已知：x=2，y=1是方程2x+3y=k的解。要求：求k的值。解答：根据题意，x=2，y=1是方程2x+3y=k的解。现在，让我们将x=2，y=1代入方程2x+3y=k，得到：2(2)+3(1)=k这意味着4+3=k7=k因此，k=7k的值为7。
要求：绘制每个给定二元线性方程的图像。解答：我们知道，要绘制二元线性方程的图像，我们需要至少两个解。(i) 找到给定方程x+y=4的解。让我们将x=0和y=0代入方程x+y=4。对于x=0，我们得到0+y=4，y=4。对于y=0，我们得到x+0=4，x=4。因此，(0, 4)和(4, 0)是方程x+y=4的两个解。因此，二元线性方程x+y=4的图像为：(ii) 找到给定方程x-y=2的解。让我们将x=0和y=0代入…… 阅读更多