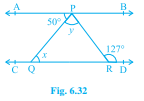
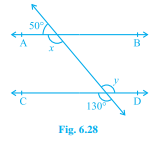
已知:AB∥CD,∠APQ=150°,∠PRD=127°。求解:我们需要求出 x 和 y。解:我们知道,如果被横截线截割的直线平行,则内错角相等。这意味着,∠APQ=∠PQR。代入数值,我们得到∠APQ=∠PRD。这意味着,x=50°。同样地,我们得到∠APR=∠PRD。代入∠PRD的值,我们得到∠APR=127°。我们知道,∠APR=∠APQ+∠QPR。现在,代入∠QPR=y 和∠APR=127°的值,我们得到127°=50°+y。这意味着,127°-50°=y,77°=y。因此,y=77°。因此,x 和 y 的值分别为 50° 和 77°。阅读更多
已知:PQ∥ST,∠PQR=130°。求解:我们需要求出∠QRS。解:让我们过点 R 作一条平行于 ST 的直线,并将其命名为 UV。我们知道,横截线同侧的角之和等于 180°。因此,∠RST+∠SRV=180°。这意味着,∠SRV=180°-130°(因为∠S=130°)。我们得到∠SRV=50°。同样地,我们得到∠PQR+∠QRU=180°。这意味着,∠QRU=180°-110°(因为∠Q=110°)。我们得到∠QRU=70°。因此,∠QRU+∠QRS+∠SRV=180°(因为线性对角的度数之和总是 180°)。因此,代入数值,我们得到∠QRS=180°-70°-50°,∠QRS=180°-120°,∠QRS=60°。因此,∠…阅读更多
已知:AB∥CD,CD∥EF,且 y:z=3:7。求解:我们需要求出 x。解:已知 AB∥CD 和 CD∥EF。我们知道,当角在横截线的同侧时,角的和总是 180°。这意味着,x+y=180°。我们也知道,两条平行线的内错角之和为 180°。这意味着,y+z=180°。令 y=3h 和 z=7h(因为 y:z=3:7)。因此,3h+7h=180°。这意味着,10h=180°,h=18°。因此,y=3×18°=54°,z=7×18°=126°。现在,将 y 的值代入 x+y=180°,我们得到 x+54°=180°,x=180°-54°=126°。因此,x=126°。阅读更多
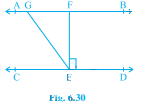
已知:AB∥CD,EF垂直于CD。∠GED = 120°。求解:我们需要求出∠GEC、∠EGF、∠GEF。解:∠GEF + ∠CEG = 120°,120° = ∠GEF + 90°,∠GEF = 120°-90°=30°。CD 是一条直线。因此,∠GED + ∠CEG = 180°,120°+∠CEG = 180°,∠CEG = 180°-120°=60°。在三角形 GFE 中,∠GFE + ∠GEF + ∠EGF = 180°,90°+30°+∠EGF = 180°,∠EGF = 180°-120°=60°。∠GEF = 30°,∠GEC = 60°,∠EGF = 60°。
已知:已知∠XYZ=64°,XY 被延长到点 P,射线 YQ 平分∠ZYP。求解:我们需要根据给定信息画一个图形,并求出∠XYQ 和∠QYP 的优角。解:XYP 是一条直线。因此,∠XYZ+∠ZYP=180°,64°+∠ZYP=180°(因为∠XYZ=64°)。这意味着,∠ZYP=180°-64°=116°。由于 YQ 平分∠ZYP,我们得到∠ZYQ=∠QYP,并且∠ZYP=2∠QYP。这意味着,116°=2∠QYP,116°/2=∠QYP,58°=∠QYP。也就是说,∠QYP=58°。因此,∠ZYQ=∠QYP=58°。类似地,我们得到∠XYQ=∠XYZ+∠ZYQ。这意味着,∠XYQ=64°+58°=122°。现在让我们求出∠QYP 的优角,∠QYP=180°+∠XYQ(因为∠QYP 是∠XYQ 的优角)。我们…阅读更多
求解:我们需要求出 x 和 y 的值,然后证明 AB∥CD。解:我们知道,线性对角的度数之和总是 180°。由于 x 和 50° 是 AB 的线性对角,我们得到 x+50°=180°。这意味着,x=180°-50°=130°。我们也知道,对顶角相等。因此,我们得到 y=130°(因为 x 和 y 是对顶角)。因此,x=y=130°。我们知道,如果内错角相等,则两条直线平行。由于 x 和 y 是内错角并且彼此相等,我们得到 AB∥CD。因此,AB∥…阅读更多
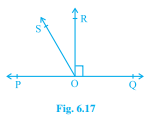
已知:POQ 是一条直线,射线 OR 垂直于直线 PQ,OS 是另一条位于射线 OP 和 OR 之间的射线。求解:我们需要证明∠ROS=1/2(∠QOS-∠POS)。解:射线 OR⊥POQ。这意味着,∠POR=90°,∠POS+∠ROS=90°……(i),∠ROS=90°-∠POS,∠POS+∠QOS=180°(线性对),=2(∠POS+∠ROS) [由(i)],∠POS+∠QOS=2∠ROS+2∠POS,2∠ROS=∠POS+∠QOS-2∠POS,2∠ROS=∠QOS…阅读更多
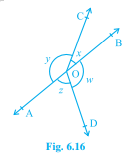
待解决问题:我们必须证明AOB是一条直线。解:我们知道,线性对角的度数之和总是180°。因此,为了证明AOB是一条直线,我们必须证明x+y是AOB的线性对。这意味着,x+y=180°我们也知道,围绕一个点的角度总和为360°。这意味着,x+y+w+z=360°因为我们有,x+y=w+z我们得到,2(x+y)=360°这意味着,x+y=360°/2x+y=180°因此,x+y是线性对这意味着,AOB是一条直线。阅读更多
已知:∠PQR=∠PRQ。待解决问题:我们必须证明∠PQS=∠PRT。解:SQRT是一条直线。我们知道,线性对角的度数之和总是180°。∠PQS+∠PQR=180° (因为它们是线性对)∠PRT+∠PRQ=180° (因为它们是线性对)因此,∠PQR=180°-∠PQS..(i)∠PRQ=180°-∠PRT....(ii)因为,∠PQR=∠PRQ我们得到,通过等式180°-∠PQS=180°-∠PRT这意味着,∠PQS=∠PRT。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP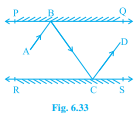 "\
"\
 "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\