已知:在直角三角形 $ABC$ 中,∠C 为直角,$M$ 是斜边 $AB$ 的中点。连接 $C$ 和 $M$,并延长到点 $D$,使得 $DM=CM$。连接 $D$ 和 $B$。要求:证明给定的问题。解答:(i) 考虑 $\triangle AMC$ 和 $\triangle BMD$,我们知道,根据边角边全等定理:如果两个三角形的一对对应边和它们的夹角相等,则这两个三角形全等。已知,$CM=DM$,且 $M$ 是斜边 $AB$ 的中点,这意味着 $AM=BM$。我们也知道,对顶角相等…… 阅读更多
已知:在等腰三角形 $ABC$ 中,$AB=A$,∠B 和∠C 的角平分线相交于点 $O$。连接 $A$ 和 $O$。要求:证明(i) $OB=OC$(ii) $AO$ 平分∠A。解答:(i) 我们知道,在等腰三角形中,所有角都相等。这意味着,∠B=∠C,1/2∠B=1/2C,这意味着,∠OBC=∠OCB。因此,由于等角的对边相等,我们得到 $OB=OC$。(ii) 考虑 $\triangle AOB$ 和 $\triangle AOC$,我们知道,根据边边边全等定理,如果一个三角形的三条边分别等于另一个三角形的三条对应边,则…… 阅读更多
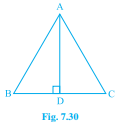
已知:在 $\triangle ABC$ 中,$AD$ 是 $BC$ 的垂直平分线。要求:证明 $\triangle ABC$ 是等腰三角形,其中 $AB=AC$。解答:考虑 $\triangle ADB$ 和 $\triangle ADC$,我们知道,根据边角边全等定理:如果两个三角形的一对对应边和它们的夹角相等,则这两个三角形全等。由于 $AD$ 是两个三角形的公共边,我们得到 $AD=DA$。这意味着,∠ADB=∠ADC。由于 $AD$ 是 $\triangle ABC$ 的垂直平分线,我们得到 $BD=CD$。因此,$\triangle ADB \cong \triangle ADC$。我们也知道,根据全等三角形的对应边:如果两个三角形全等,则它们的对应边必须相等。因此…… 阅读更多
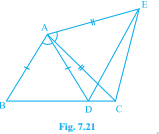
已知:$AC=AE, AB=AD$ 和 $\angle BAD=\angle EAC$。要求:证明 $BC=DE$。解答:在 $\angle BAD=\angle EAC$ 的两边都加上 $\angle DAC$,我们得到,$\angle BAD+\angle DAC=\angle EAC+\angle DAC$。这意味着,$\angle BAC=\angle EAD$。我们知道,根据边角边全等定理:如果两个三角形的一对对应边和它们的夹角相等,则这两个三角形全等。已知,$AC=AE$ 和 $AB=AD$。我们还有,$\angle BAC=\angle EAD$。因此,$\angle ABC \cong \angle ADE$。我们也知道,根据全等三角形的对应边:如果两个三角形全等,则它们的对应边必须相等。因此,$BC=DE$。阅读更多
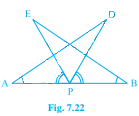
已知:$AB$ 是一条线段,$P$ 是它的中点。$D$ 和 $E$ 是 $AB$ 同侧上的点,使得 $\angle BAD=\angle ABE$ 和 $\angle EPA=\angle DPB$。要求:证明(i) $\triangle DAP \cong \triangle EBP$(ii) $AD=BE$。解答:(i) 在 $\angle EPA=\angle DPB$ 的两边都加上 $\angle DPE$,我们得到,$\angle EPA+\angle DPE=\angle DPB+\angle DPE$。这意味着,$\angle DPA=\angle EPB$。现在,考虑 $\triangle DAP$ 和 $EBP$。我们有,$DPA=EPB$。我们也知道,$P$ 是线段 $AB$ 的中点。这意味着,$AP=BP$。由于 $\angle BAD=\angle ABE$。因此,根据角边角定理:如果两个三角形的两个角和它们的夹边…… 阅读更多
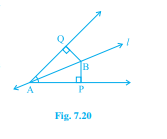
已知:直线 $l$ 是角 $\angle A$ 的角平分线,且 $B$ 是 $l$ 上的任意一点。$BP$ 和 $BQ$ 是从 $B$ 到 $\angle A$ 的两边的垂线。要求:证明(i) $\triangle APB \cong \triangle AQB$(ii) $BP=BQ$ 或 $B$ 到 $\angle A$ 的两边的距离相等。解答:(i) 我们知道,根据角边角定理:如果两个三角形的两个角和它们的夹边分别相等,则这两个三角形全等。这意味着,∠P=∠Q 且 $AB=BA$。由于直线 $l$ 是∠A 的角平分线,我们得到,∠BAP=…… 阅读更多
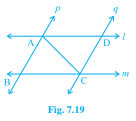
已知:$l$ 和 $m$ 是两条平行线,被另一对平行线 $p$ 和 $q$ 所截。要求:证明 $\triangle ABC\cong \triangle CDA$。解答:考虑 $\triangle ABC$ 和 $\triangle CDA$,我们知道,当被截线平行时,内错角相等。这意味着,∠BCA=∠DAC 和 ∠BAC=∠DCA。由于 $AC$ 和 $CA$ 是两个三角形的公共边,我们得到 $AC=CA$。因此,根据角边角定理:如果两个三角形有两对角和它们的夹边分别相等,则这两个三角形全等。我们得到,$\triangle ABC …… 阅读更多
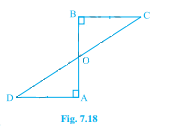
已知:$AD$ 和 $BC$ 是线段 $AB$ 的两个相等垂线。
(a) 空气 - 混合物 (b) 铜 - 纯净物 (c) 银 - 纯净物 (d) 糖水 - 混合物 (e) 风 - 混合物 (f) 盐水 - 混合物 (g) 二氧化碳 - 纯净物 (h) 水 - 纯净物 (i) 氮气 - 纯净物 (j) 铁 - 纯净物 (k) 氧气 - 纯净物 (l) 牛奶 - 混合物 (m) 血液 - 混合物 (n) 金 - 纯净物 (o) 黄铜 - 混合物

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP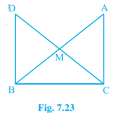 "
"

 "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\