数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学
题目：我们必须证明等边三角形的三个角都是60°。解答：让我们考虑一个等边三角形ABC，我们有AB=BC=AC（如图所示）。我们知道，等角对等边。因此，∠A=∠B=∠C。我们也知道，三角形的内角和总是等于180°。这意味着在△ABC中，∠A+∠B+∠C = 180°。因此，3∠A=180°（因为∠A=∠B=∠C），∠A=180°/3，∠A=60°。因此，∠A=∠B=∠C=60°。因此，等边三角形的三个角都是60°。阅读更多
已知：ABC是一个直角三角形，其中∠A=90°，且AB=AC。题目：我们必须求出∠B和∠C。解答：已知AB=AC。我们知道，等边对等角。这意味着∠B=∠C。我们知道，三角形的内角和总是等于180°。这意味着在△ABC中，∠A+∠B+∠C=180°。因此，90°+2∠B=180°（因为∠B=∠C）。这意味着2∠B=90°，∠B=90°/2，∠B=45°。因此，∠B=∠C=45°。阅读更多
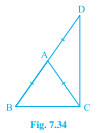
"\已知：△ABC是一个等腰三角形，其中AB=AC。边BA延长到D，使得AD=AB。题目：我们必须证明∠BCD是直角。解答：让我们考虑△ABC，已知AB=AC。我们知道，等边对等角。这意味着∠ACB=∠ABC。现在，让我们考虑△ACD，已知AD=AB。我们知道，等边对等角。这意味着∠ADC=∠ACD。我们知道，三角形的内角和总是等于180°。这意味着在△ABC中，…阅读更多
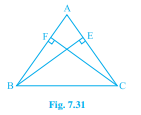
"\已知：ABC是一个三角形，其中对边AC和AB的高BE和CF相等。题目：我们必须证明：(i) △ABE ≅ △ACF (ii) AB=AC，即ABC是等腰三角形。解答：(i) 我们知道，如果一个三角形的两个角和一个非夹边等于另一个三角形的对应角和非夹边，则这两个三角形全等。已知BE=CF。我们有∠A是AEB和AFC的公共角。∠AEB=∠AFC。因此，△AEB ≅ △AFC。我们也知道，根据全等三角形的对应部分：如果两个三角形全等，则它们的所有…阅读更多
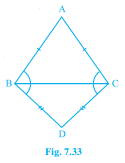
"\已知：ABC和DBC是同底BC上的两个等腰三角形。题目：我们必须证明∠ABD=∠ACD。解答：让我们考虑△ABD和△ACD。我们知道，边边边全等定理指出，如果一个三角形的三个边分别等于另一个三角形的三个对应边，则这两个三角形全等。由于AD是两个三角形的公共边，我们得到AD=DA。由于ABC和DBC是两个等腰三角形，我们得到AB=AC和BD=CD。因此，∠ABD ≅ ∠ACD。我们也知道，根据全等三角形的对应部分：如果两个三角形全等，则它们的所有…阅读更多
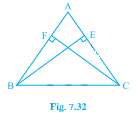
"\已知：ABC是一个等腰三角形，其中对等边AC和AB分别作高BE和CF。题目：我们必须证明这些高相等。解答：让我们考虑△AEB和△AFC。我们知道，根据角角边定理：如果一个三角形的两个角和一个非夹边等于另一个三角形的对应角和非夹边，则这两个三角形全等。AB=AC（已知）。我们有∠A是AEB和AFC的公共角。∠AEB=∠AFC。因此，△AEB ≅ △AFC。我们也知道，根据全等三角形的对应部分：如果两个三角形全等，则它们的所有…阅读更多
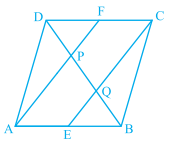
"\已知：在平行四边形ABCD中，E和F分别是AB和CD的中点。
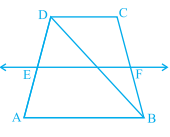
"\已知：ABCD是一个梯形，其中AB∥DC，BD是对角线，E是AD的中点。一条平行于AB的直线穿过E，与BC相交于F。
已知：ABC是一个直角三角形，∠C=90°。一条通过斜边AB中点M且平行于BC的直线与AC相交于D。
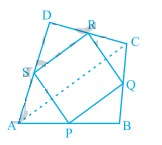
"\已知：ABCD是一个四边形，其中P、Q、R和S分别是AB、BC、CD和DA的中点。AC是对角线。