已知:PR > PQ 且 PS 平分∠QPR。要证明:∠PSR > ∠PSQ。证明:在△PQR 中,PR > PQ,则∠PQR > ∠PRQ。(i) 因为 PS 平分∠QPR,所以∠QPS = ∠RPS。(ii) 在△PSR 中,∠PSR = ∠PQR + ∠QPS;在△PSQ 中,∠PSQ = ∠PRQ + ∠RPS。(iii) (i) + (ii) 得 ∠PQR + ∠QPS > ∠PRQ + ∠RPS,所以… 阅读更多
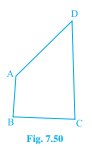
已知:AB 和 CD 分别是四边形 ABCD 的最短边和最长边。要证明:∠A > ∠C 且∠B > ∠D。证明:在△ABD 中,AB < AD,则∠ADB < ∠ABD。(i) 同理,在△BCD 中,BC < CD,则∠BDC < ∠DBC。(ii) (i) + (ii) 得 ∠ADB + ∠BDC < ∠ABD + ∠DBC,即∠ADC < ∠B,所以∠B > ∠D。同理,在△ABC 中… 阅读更多
已知:∠B
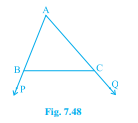
已知:△ABC 的边 AB 和 AC 分别延长到点 P 和 Q。此外,∠PBC < ∠QCB。证明:AC > AB。解:∠ABC + ∠PBC = 180°,∠ABC = 180° - ∠PBC;∠ACB + ∠QCB = 180°,∠ACB = 180° - ∠QCB。已知 ∠PBC < ∠QCB,所以 ∠ABC > ∠ACB。在三角形中,大角对大边,所以 AC > AB。
证明:在直角三角形 ABC 中,∠A + ∠B + ∠C = 180°,∠A = 90°,所以 ∠B + ∠C = 90°。∠A 是最大角,所以对边 BC(斜边)是最长边。阅读更多
已知:BE 和 CF 是三角形 ABC 的两个相等的垂线。证明:在Rt△BEC和Rt△CFB中,BE=CF,BC=CB,∠BEC=∠CFB=90°,根据RHS全等,Rt△BEC≌Rt△CFB,所以 CE=BF。所以 AB=AC,三角形 ABC 是等腰三角形。阅读更多
已知:ABC 是一个等腰三角形,其中 AB=AC。证明:在Rt△APB和Rt△APC中,AB=AC,AP=AP,∠APB=∠APC=90°,根据RHS全等,Rt△APB≌Rt△APC,所以∠B=∠C。阅读更多
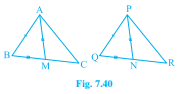
已知:三角形 ABC 的两边 AB 和 BC 以及中线 AM 分别等于三角形 PQR 的边 PQ 和 QR 以及中线 PN。证明:(i) △ABM ≅ △PQN (ii) △ABC ≅ △PQR。证明:(i) 因为 AM 和 PN 是中线,所以 BM = BC/2 和 QN = QR/2。由于 BC = QR,所以 BM = QN。在△ABM 和△PQN 中,AB = PQ,BM = QN,AM = PN,根据 SSS 全等,△ABM ≅ △PQN。(ii) …阅读更多
已知:AD 是等腰三角形 ABC 的高,AB=AC。证明:(i) AD 平分 BC (ii) AD 平分∠A。证明:在Rt△ABD和Rt△ACD中,AB=AC,AD=AD,∠ADB=∠ADC=90°,根据RHS全等,Rt△ABD ≅ Rt△ACD,所以 BD=CD,AD 平分 BC。又因为 Rt△ABD ≅ Rt△ACD,所以∠BAD=∠CAD,AD 平分∠A。阅读更多
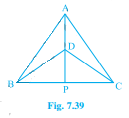
已知:△ABC和△DBC是同底BC的两个等腰三角形,顶点A和D在BC的同侧。AD延长线与BC相交于点P。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP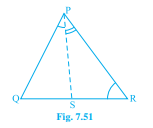 "\
"\
 "\
"\ "
" "\
"\ "\
"\ "
"