证明等边三角形的三个角都为60°。

待办事项

我们必须证明等边三角形的三个角都为60°。

解答

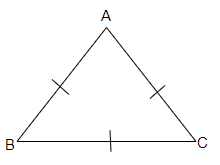
让我们考虑一个等边三角形ABC

我们有：

AB=BC=AC (根据图示)

我们知道：

等角对等边。

因此：

∠A=∠B=∠C

我们也知道：

三角形的内角和始终等于180°

这意味着

在△ABC中：

∠A+∠B+∠C = 180°

因此：

3∠A=180° (因为∠A=∠B=∠C)

∠A=180°/3

∠A= 60°

因此：

∠A=∠B=∠C=60°

因此，等边三角形的三个角都为60°。

教程点

更新于：2022年10月10日

60次浏览

开启你的职业生涯

完成课程获得认证

开始学习