已知:△PQR 的边 QR 延长到点 S。∠PQR 和∠PRS 的平分线相交于点 T。 求证:∠QTR = 1/2∠QPR。证明:考虑∠PQR,我们知道内角和等于外角。这里,∠PRS 是外角,∠QPR 和∠PQR 是内角。因此,∠PRS = ∠QPR + ∠PQR,这意味着 ∠PRS - ∠PQR = ∠QPR。现在,考虑△QRT,同样地,我们得到∠TRS = ∠TQR + ∠QTR,这意味着∠QTR = ∠TRS - ∠TQR……(a) 由于 QT 和 RT 平分∠PQR ... 阅读更多
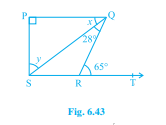
已知:PQ⊥PS,∠SQR=28° 和 ∠QRT=65°。求解:我们需要找到 x 和 y 的值。解:因为 QR 是一条横截线,所以内错角相等。x + ∠SQR = ∠QRT,代入∠QRT 和∠SQR 的值,我们得到 x + 28° = 65°,x = 65° - 28°,x = 37°。我们也知道,被横截线截成的平行线,内错角相等。∠QSR = 37°。我们知道,线性对角的度数之和总是 180°。因此,∠QRS + ∠QRT = 180°,∠QRS + 65° = 180°,这意味着 ∠QRS = 180° - 65°,∠QRS = 115°。利用三角形 SPQ 的内角和性质,∠SPQ + x + y = 180°,90° + 37° + y = 180°,y = 180° - 127°,y = 53°。因此,y = 53°。阅读更多
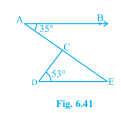
已知:AB∥DE,∠BAC=35° 和 ∠CDE=53°。求解:我们需要找到∠DCE。解:我们知道,直线 AB∥DE。因此,AE 成为 AB 和 DE 的横截线。由于被横截线截成的直线平行,内错角相等。这意味着∠BAC = ∠AED。由于∠BAC = 35°,我们得到∠AED = 35°。同样地,在△CDE 中,我们得到∠DCE + ∠CED + ∠CDE = 180°(因为三角形的内角和为 180°)。代入数值,我们得到∠DCE + ∠CED + 53° = 180°。由于∠BAC = 35°,我们也得到∠CED = 35°(内错角)。因此,∠DCE + 35° + 53° = 180°,∠DCE + 88° = 180°,... 阅读更多
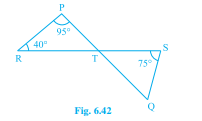
已知:直线 PQ 和 RS 相交于点 T,∠PRT=40°,∠RPT=95° 和 ∠TSQ=75°。求解:我们需要找到∠SQT。解:考虑△PRT。我们知道,三角形的内角和总是 180°。因此,∠PRT + ∠RPT + ∠PTR = 180°。代入∠PRT 和∠RPT 的值,我们得到 95° + 40° + ∠PTR = 180°,135° + ∠PTR = 180°,这意味着∠PTR = 180° - 135°,∠PTR = 45°。我们知道,在三角形中,对顶角总是相等的。这意味着∠PTR = ∠STQ,∠STQ = 45°。由于三角形的内角和总是 180°,我们得到∠TSQ + ∠PTR + ∠SQT = 180°。... 阅读更多
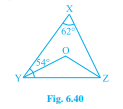
已知:∠X=62°,∠XYZ=54°。YO 和 ZO 分别是△XYZ 的∠XYZ 和∠XZY 的平分线。求解:我们需要找到∠OZY 和∠YOZ。解:我们知道三角形的内角和总是 180°。这意味着∠X + ∠XYZ + ∠XZY = 180°。代入 X 和 Y 的值,我们得到 62° + 54° + ∠XZY = 180°,这意味着 116° + ∠XZY = 180°,∠XZY = 180° - 116°,∠XZY = 64°。我们知道,YO 和 ZO 分别是△XYZ 的∠XYZ 和∠XZY 的平分线。因此,我们得到∠OYZ = 1/2∠XZY,∠OYZ = 54°/2,∠OYZ = 27°。同样地,我们得到∠OZY = 1/2∠XZY,∠OZY = 64°/2,∠OZY = 32°。由于我们知道... 阅读更多
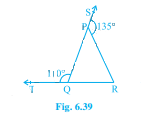
已知:△PQR 的边 QP 和 RQ 分别延长到点 S 和 T。∠SPR=135° 和 ∠PQT=110°。求解:我们需要找到∠PRQ。解:我们知道,线性对角的度数之和总是 180°。这意味着∠TQP + ∠PQR = 180°。代入∠TQP 的值,我们得到 110° + ∠PQR = 180°,这意味着∠PQR = 180° - 110°,∠PQR = 70°。我们也知道,内角和等于外角。从△PQR,我们得到∠PQR + ∠PRQ = 135°。代入∠PQR 的值,我们得到∠PRQ = 135° - 70°,这意味着∠PRQ = 65°。因此,∠PRQ = 65°。阅读更多
求解:我们需要找出点 (-2, 4)、(3, -1)、(-1, 0)、(1, 2) 和 (-3, -5) 位于哪个象限或哪个轴上。解:为了找到点 (-2, 4), (3, -1), (-1, 0), (1, 2) 和 (-3, -5) 的象限或轴,请在图表上绘制这些点,如下所示。从上图中,我们可以得出结论:点 (-2, 4) 位于第二象限。点 (3, -1) 位于第四象限。点 (-1, 0) 位于负 X 轴上。点 (1, 2) 位于第一象限。点 (-3, -5) 位于第三象限。
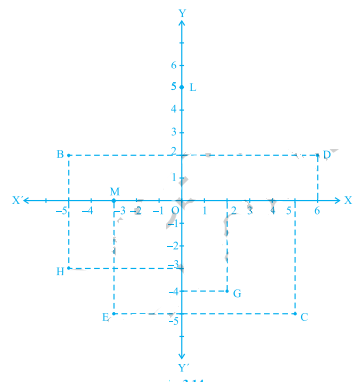
求解:(i) B 点的坐标。(ii) C 点的坐标。(iii) 坐标为 (-3, -5) 的点。(iv) 坐标为 (2, -4) 的点。(v) D 点的横坐标。(vi) H 点的纵坐标。(vii) L 点的坐标。(viii) M 点的坐标。解:从图中,我们可以观察到:(i) B 点的 X 坐标是它到 Y 轴的距离,B 点的 Y 坐标是它到 X 轴的距离。因此,B 点的坐标为 (-2, 5)。(ii) C 点的 X 坐标是它到 Y 轴的距离,... 阅读更多
待解决:我们必须找出 (i) 可以被称为\( (4, 3) \)的交叉街道数量。(ii) 可以被称为\( (3, 4) \)的交叉街道数量。解答:绘制两条垂直线作为城市的两条主要街道,它们在中心交叉。将它们标记为南北方向(用 N 和 S 表示)和东西方向(用 E 和 W 表示)。给定的比例尺为 $1\ cm = 200\ m$。绘制五条与两条主干道平行的街道。因此,街道规划如下图所示。从上图中,我们可以得出结论:(i) 只有… 阅读更多
待解决:我们必须回答给定的问题。解答:(i) 用于确定笛卡尔平面中任何点位置的水平线称为X轴。用于确定笛卡尔平面中任何点位置的垂直线称为Y轴。(ii) 由X轴和Y轴形成的平面的每个部分称为象限。(iii) X轴和Y轴相交的点称为原点 O。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP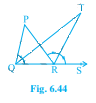 "\
"\
 "\
"\ "\
"\ "\
"\ "\
"\ "\
"\