点\( (-2,4),(3,-1),(-1,0) \), \( (1,2) \) 和 \( (-3,-5) \) 分别位于哪个象限或哪条坐标轴上？通过在笛卡尔平面中定位这些点来验证你的答案。

待办事项

我们需要找到点\( (-2,4),(3,-1),(-1,0) \), \( (1,2) \) 和 \( (-3,-5) \) 位于哪个象限或哪条坐标轴上。

解答： 

为了找到点$(-2, 4), (3, -1), (-1, 0), (1, 2)$ 和 $(-3, -5)$ 所在的象限或坐标轴，我们将这些点绘制在图上，如下所示。


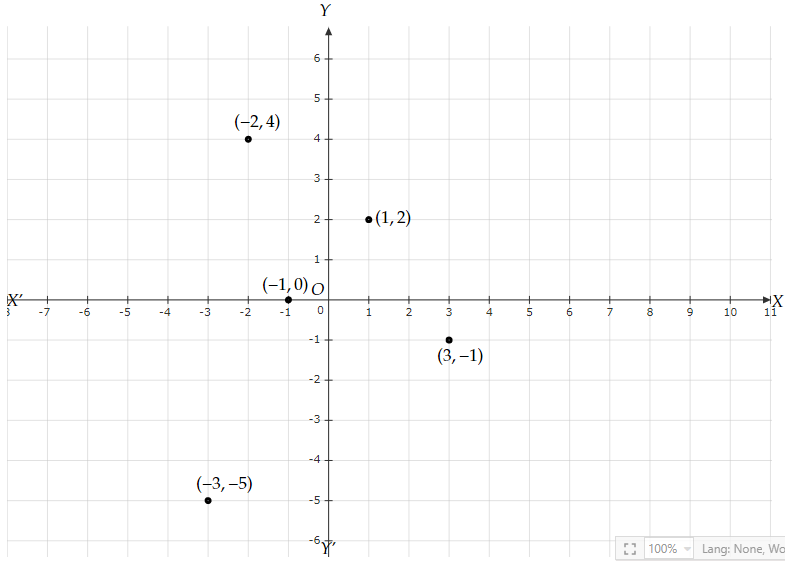
从上图中，我们可以得出以下结论：

点 $(-2, 4)$ 位于第 $2$ 象限。

点 $(3, -1)$ 位于第 $4$ 象限。

点 $(-1, 0)$ 位于负 X 轴上。

点 $(1, 2)$ 位于第 $1$ 象限。

点 $(-3, -5)$ 位于第 $3$ 象限。

更新于： 2022年10月10日

1K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告