16. 在笛卡尔坐标系中绘制以下每个点
(a) (3, 4)
(b) (-3, -4)
(c) (0, -5)
(d) (2, -5)
(e) (2, 0)
在笛卡尔坐标系中绘制以下每个点：
(a) (3, 4)
(b) (-3, -4)
(c) (0, -5)
(d) (2, -5)
(e) (2, 0)
答案
以上每个点都已绘制在下面的笛卡尔坐标系中
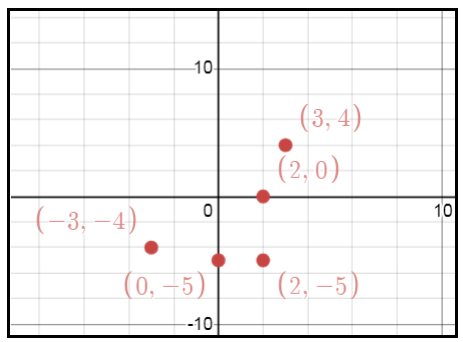
- 相关文章
- 解下列方程：(a). 4=5(p−2)(b). −4=5(p−2)(c). 16=4+3(t+2)(d). 4+5(p−1)=34(e). 0=16+4(m−6)
- 从下列每个展开式中找出数字：(a). 8×104+6×103+0×102+4×101+5×100(b). 4×104+5×103+3×102+2×100(c). 3×104+7×102+5×100(d). 9×105+2×102+3×101
- 下列数据给出了41个家庭的孩子数量：1,2,6,5,1,5,1,3,2,6,2,3,4,2,0,0,4,4,3,2,2,0,0,1,2,2,4,3,2,1,0,5,1,2,4,3,4,1,6,2,2.将其表示为频数分布的形式。
- 化简并将下列每个表达式表示为指数形式：(i). 23×34×43×32(ii). [(52)3 ×54]÷57(iii). (254÷53)(iv). 3×72×11821×113(v). 3734×33(vi). 20+30+40(viii). 20×30×40(viii). (30+20)×50(ix). 28×a543×a3(x). (a5a3)×a8(xi). 45×a8b345×a5b2(xii). (23×2)2
- 化简下列式子：a. 3×102 b. 25×53c. 0×104
- 化简并将答案写成指数形式。(a) 3×310(b) 52×57(c) (−7)2×(−7)7(d) 273\p39(e) (250+50)×50(f) (20\p30)×40
- 证明点A(1,0),B(5,3),C(2,7)和D(−2,4)是平行四边形的顶点。
- 证明点(3,−2),(4,0),(6,−3)和(5,−5)是平行四边形的顶点。
- 命名由以下点形成的四边形类型（如果存在），并说明你的答案的原因。(i) (−1,−2),(1,0),(−1,2),(−3,0)(ii) (−3,5),(3,1),(0,3),(−1,−4)(iii) (4,5),(7,6),(4,3),(1,2)
- 从下列问题的四个选项中选择正确的答案：以下哪个方程没有实根？（A）x2−4x+3√2=0(B) x2+4x−3√2=0(C) x2−4x−3√2=0(D) 3x2+4√3x+4=0
- 解下列方程：(a). 2(x+4)=12(b). 3(n−5)=21(c). 3(n−5)=−21(d). −4(2+x)=8(e). 4(2−x)=8
- 计算下列式子：(30−20)×50
- 证明A(−3,2),B(−5,−5),C(2,−3)和D(4,4)是菱形的顶点。
- 将下列比率转换为百分比：(a). 3:1, (b). 2:3:5, (c). 1:4, (d). 1:2:5。
- 从下列问题的四个选项中选择正确的答案：以下哪个方程有两个不同的实根？（A）2x2−3√2x+94=0(B) x2+x−5=0(C) x2+3x+2√2=0(D) 5x2−3x+1=0
数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
服装研究
法律研究