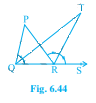
如图 6.44 所示，△PQR 的边 QR 延长到点 S。如果∠PQR 和∠PRS 的角平分线相交于点 T，则证明∠QTR = ½∠QPR

已知

△PQR 的边 QR 延长到点 S。

∠PQR 和∠PRS 的角平分线相交于点 T。

要求

我们必须证明∠QTR = ½∠QPR。

解答

让我们考虑∠PQR

我们知道：

内角和等于外角。

这里，∠PRS 是外角，

∠QPR 和∠PQR 是内角。

因此，

∠PRS = ∠QPR + ∠PQR

这意味着：

∠PRS - ∠PQR = ∠QPR

现在，让我们考虑△QRT

同样地，我们得到：

∠TRS = ∠TQR + ∠QTR

这意味着：

∠QTR = ∠TRS - ∠TQR ......(a)

由于 QT 和 RT 分别平分∠PQR 和∠PRS，我们得到：

∠PRS = 2∠TRS 和 ∠PQR = 2∠TQR

因此，

∠QTR = ½∠PRS - ½∠PQR

这意味着：

∠QTR = ½(∠PRS - ∠PQR)

从公式 (a) 我们知道 ∠PRS - ∠PQR = ∠QPR

因此，

∠QTR = ½∠QPR

证毕。

Tutorialspoint

更新于：2022年10月10日

浏览量 36 次

开启你的职业生涯

完成课程获得认证

开始学习