数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
要做的：我们必须给出理由来证明公理 5 是普遍真理。解决方案：例如：让我们考虑一个西瓜。当它完整或完整时，它重 1 公斤。现在，让我们取一部分并吃掉它。然后，如果我们称量剩下的部分，它的重量将小于整体的重量。因此，整体总是大于部分。因此得证。
要做的：我们必须改写欧几里得第五公设。解决方案：欧几里得第五公设：如果一条直线落在两条直线上，使得它同侧的内角之和小于两个直角，则这两条直线无限延长后，将在内角和小于两个直角的一侧相交。因此，欧几里得第五公设是关于平行线的。我们知道，在几何学中，平行线可以定义为同一平面内距离相等且永不相交的两条线。(i) 如果 P 不在直线上 ... 阅读更多
要做的：我们必须解释欧几里得第五公设是否暗示平行线的存在。解决方案：是的，欧几里得第五公设确实暗示了平行线的存在。当内角和等于直角和时，这两条直线在任何给定点都不会相交。因此，这些线彼此平行。
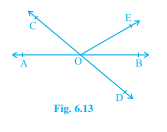
"\已知：直线 AB 和 CD 在 O 处相交。∠AOC + ∠BOE = 70° 且 ∠BOD = 40°要做的：我们必须找到 ∠BOE 和优角 ∠COE。解决方案：AOB 是一条直线。因此，∠AOC + ∠COE + ∠BOE = 180°(∠AOC + ∠BOE) + ∠COE = 180°70° + ∠COE = 180°∠ COE = 180°-70°= 110°∠ AOC = ∠ BOD = 40° (对顶角)∠AOC + ∠BOE = 70°这意味着，∠BOD + ∠BOE = 70°∠ BOE = 70° - 40° = 30°优角 ∠COE = 360° - ∠COE= 360°-... 阅读更多
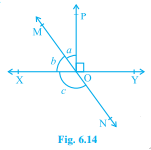
"\已知：XY、MN 在 O 处相交，∠POY=90° 且 a:b=2:3。要做的：我们必须找到 c。解决方案：已知，∠POY=90° 且 a:b=2:3我们知道，线性对角的度数之和始终为 180°。这意味着，∠POY+a+b=180°通过将 ∠POY=90° 代入上述方程式我们得到，90°+a+b=180°a+b=180°-90°a+b=90°设 a 为 2x，b 为 3x（因为，a:b=2:3）这意味着，2x+3x=90°5x=90°x=90°/5x=18°因此，a=2×18°a=36°和b=3×18°b=54°类似地，由于 b 和 c 也在一条直线上我们得到，b+c=180°这意味着，54°+c=180°c=180°-54°c=126°因此，c=126°。阅读更多
"\已知：AC=BD。要做的：我们必须证明 AB=CD。解决方案：已知，AC=BD根据图，我们得到，AC=AB+BCBD=BC+CD这意味着，AB+BC=BC+CD....(i) (因为，AC=BD根据欧几里得公理，当从相等中减去相等时，余数也相等。因此，让我们从 (i) 的两边减去 BC我们得到，AB+BC-BC=BC+CD-BC这意味着，AB=CD因此得证。
已知：点 C 是 AB 的中点。要做的：我们必须证明每条线段都有一个且只有一个中点。解决方案：假设点 C 和 D 是 AB 的两个中点。由于 C 和 D 是 AB 的中点。我们得到，AC=CB 和 AD=BD根据欧几里得公理我们得到，AC+CB=AB (因为，AC+CB 与 AB 重合)类似地，我们得到，AD+BD=AB (因为，AD+BD 与 AB 重合)现在， 通过在 AC=CB 的两边加上 AC我们得到，AC+AC=CB+AC（因为，如果相等加到相等上，则整体相等。）这意味着，2AC=AB...........(i)以类似的方式，我们得到，AD+AD=DB+AD (因为，如果相等加到相等上，则整体相等... 阅读更多
要做的：我们必须为每个给定的术语给出定义，以及首先需要定义的其他术语。解决方案：是的，还有其他术语和点需要首先定义，然后我们才能定义给定的术语。直线：直线可以定义为只有长度而没有宽度的点的集合。直线可以在两侧无限延伸。平面：平面是无限延伸的平面二维表面，可以在其中绘制几何图形。点：在几何学中，点是用小点表示的位置，它没有长度也没有宽度。圆：在 ... 阅读更多
要做的：我们必须考虑给定的公设。解决方案：是的，这些公设包含未定义的术语。C 的位置没有定义。点是否位于连接 AB 的线段上。公设中提到的所有点是否都在同一个平面上。是的，这些公设是一致的，因为对于同一个未定义术语（点 c）有两种不同的情况。不，它们不来自欧几里得的公设。它们遵循公理之一。也就是说，给定任意两点，有一条唯一的直线通过它们。
已知：点 C 位于两点 A 和 B 之间，使得 AC=BC。要做的：我们必须证明 AC=1/2AB。解决方案：已知，AC=BC通过在两边加上 AC 我们得到，AC+AC=BC+AC这意味着，2AC=BC+AC (BC+AC 与 AB 重合)根据欧几里得公理 4BC+AC=AB。因此，2AC=AB这意味着，AC=1/2AB