绘制下列每个二元一次方程的图像
(i) \( x+y=4 \)
(ii) \( x-y=2 \)
(iii) \( y=3 x \)
(iv) \( 3=2 x+y \).
要做的事情
我们必须绘制每个给定二元一次方程的图像。
解答
我们知道:
要绘制二元一次方程的图像,我们需要至少两个方程的解。
(i) 寻找给定方程\(x+y=4\)的解。
让我们在方程\(x+y=4\)中代入\(x=0\)和\(y=0\)
对于\(x=0\)
我们得到:
\(0+y=4\)
\(y=4\)
对于\(y=0\)
我们得到:
\(x+0=4\)
\(x=4\)
因此:
\( (0, 4) \)和\( (4, 0) \)是方程\(x+y=4\)的两个解。
因此:
二元一次方程\(x+y=4\)的图像为:

(ii) 寻找给定方程\(x-y=2\)的解。
让我们在方程\(x-y=2\)中代入\(x=0\)和\(y=0\)
对于\(x=0\)
我们得到:
\(0-y=2\)
\(y=-2\)
对于\(y=0\)
我们得到:
\(x-0=2\)
\(x=2\)
因此:
\( (0, -2) \)和\( (2, 0) \)是方程\(x-y=2\)的两个解。
因此:
二元一次方程\(x-y=2\)的图像为:
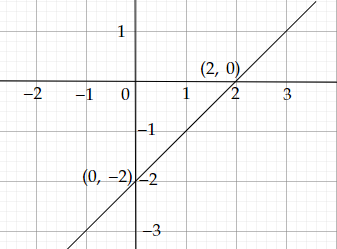
(iii) 寻找给定方程\(y=3x\)的解。
让我们在方程\(y=3x\)中代入\(x=0\)和\(y=3\)
对于\(x=0\)
我们得到:
\(y=3(0)\)
\(y=0\)
对于\(y=3\)
我们得到:
\(3=3x\)
\(3x=3\)
\(x=1\)
因此:
\( (0, 0) \)和\( (1, 3) \)是方程\(y=3x\)的两个解。
因此:
二元一次方程\(y=3x\)的图像为:
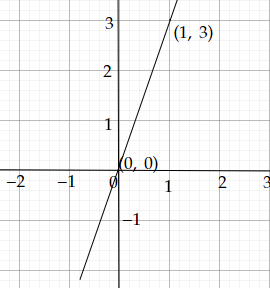
(iv) 寻找给定方程\(3=2x+y\)的解。
让我们在方程\(3=2x+y\)中代入\(x=0\)和\(y=1\)
对于\(x=0\)
我们得到:
\(3=2(0)+y\)
\(3=0+y\)
\(3=y\)
对于\(y=1\)
我们得到:
\(3=2x+1\)
\(3-1=2x\)
\(2=2x\)
\(x=1\)
因此:
\(x=1\)
因此:
\( (0, 3) \)和\( (1, 1) \)是方程\(3=2x+y\)的两个解。
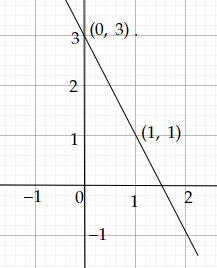


 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP