数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究
旋转对称性 旋转对称性是指图形旋转一定角度后仍然保持不变的特性。物体的旋转对称次数是其在每次旋转后外观完全相同的不同方向的数量。是的，当一个图形有两条或多条对称轴时，它具有大于1阶的旋转对称性，因为穿过中心的每条线都构成一条对称轴，并且它围绕中心以每个角度进行旋转对称。例如：等边三角形有三条对称轴。它在$120^{\circ}$、$240^{\circ}$…角度显示旋转对称性。 阅读更多
题目：说出任何两个同时具有线对称性和旋转对称性的图形。解答：线对称性：‘线对称性’是我们可以折叠图像并使两半完全匹配的假想线。旋转对称性：旋转对称性是图形旋转一定角度后仍然保持不变的特性。物体的旋转对称次数是其在每次旋转后外观完全相同的不同方向的数量。同时具有线对称性和旋转对称性的图形：等腰三角形就是这样一种既具有线对称性又具有旋转对称性的图形。正方形也是这样一种…… 阅读更多
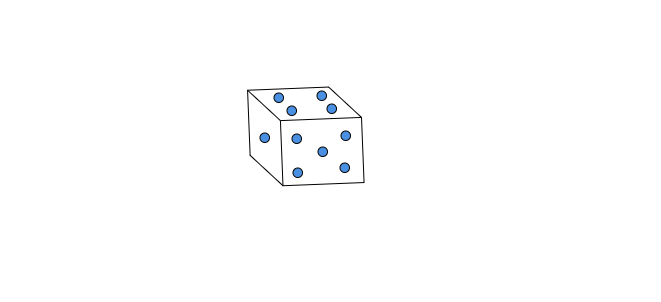
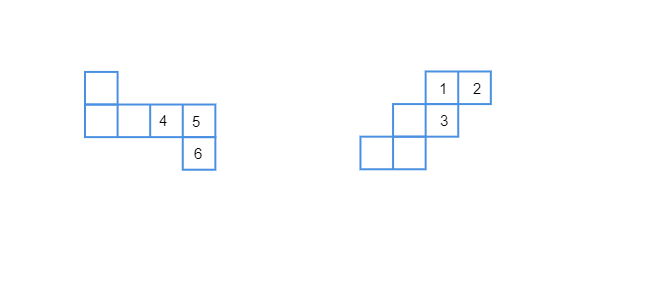
已知：制作骰子（立方体）的两个展开图。题目：用合适的数字填充展开图中的空格。解答：骰子是立方体形状的固体，每个面上都有点。相对面上的数字之和应为 7。在第一个图中：第一个空格恰好与标有 6 的正方形相对。因此，我们将 1 填入第一个空格。第二个空格的对面标有 4。因此，我们将 7-4=3 填入第二个空格。第三个空格与标有 5 的正方形相对。因此，我们将 2 填入第三个空格。在第二个图中：第一个空格…… 阅读更多
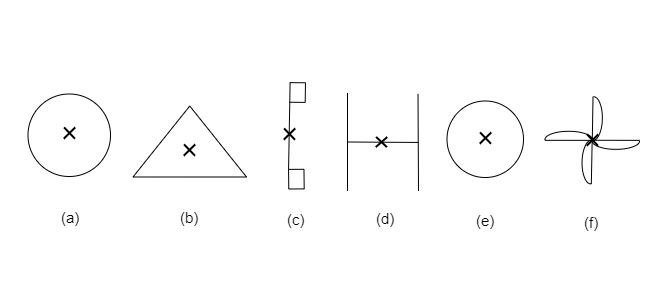
"\旋转对称性：- 当物体绕中心旋转一定角度时，物体看起来仍然相同。这被称为物体的旋转对称性。对称阶数是物体在$360^{\circ}$旋转中看起来相同的位置数量。大于一阶的旋转对称性是：(a)、(b)、(d)、(e)和(f)，因为在这些图形中，在完整旋转中，物体看起来不止一次完全相同。
当一个图形沿其对称轴对折时，两半完全重合。这条对称轴称为对称轴。(a)。等边三角形有三条对称轴。(b)。等腰三角形有一条对称轴。(c)。不等边三角形没有对称轴。(d)。正方形有四条对称轴。(e)。长方形有两条对称轴。(f)。菱形有两条对称轴。(g)。平行四边形没有对称轴。(h)。四边形没有对称轴。(i)。正六边形有六条对称轴。(j)。圆形有无数条对称轴。阅读更多
题目：我们要找出给定的多项式中哪些是单变量的，哪些不是，并说明原因。解答：(i) 在 $4x^2−3x+7$ 中，$x$ 的所有幂都是整数。因此，它是一个单变量 $x$ 的多项式。(ii) 在 $y^2+\sqrt2$ 中，$y$ 的幂是一个整数。因此，它是一个单变量 $y$ 的多项式。(iii) $3\sqrt{t}+t\sqrt{2}$ 可以写成 $3t^{\frac{1}{2}}+ t\sqrt2$。第一项的指数是 $\frac{1}{2}$，它不是整数。因此，它不是多项式。(iv) 在 $y+\frac{2}{y}=y+2y^{-1}$ 中，第二项的指数是 $-1$，它不是整数。因此，它不是…… 阅读更多
题目：我们要找出每个表达式中 $x^2$ 的系数。解答：系数：系数是数字和变量乘积的数字部分。因此，(i) \( 2+x^{2}+x \) 可以写成 $1\times x^2+1\times x+2$。这里，$x^2$ 乘以 1。因此，该表达式中 $x^2$ 的系数是 1。(ii) \( 2-x^{2}+x^{3} \) 可以写成 $1\times x^3-1\times x^2+2$。这里，$x^2$ 乘以 -1。因此，该表达式中 $x^2$ 的系数是 -1。(iii) \( \frac{\pi}{2} x^{2}+x \) 可以写成 $\frac{\pi}{2}\times x^2+1\times x$。这里，$x^2$ 乘以 $\frac{\pi}{2}$。因此，该表达式的系数…… 阅读更多
待办事项：我们需要写出每个给定多项式的次数。解答：多项式的次数：多项式的次数是多项式中变量的最高次幂。因此，(i) 在 $5x^3 + 4x^2 + 7x^1$ 中，$5x^3$ 的变量次幂为 3，$4x^2$ 的变量次幂为 2，$7x^1$ 的变量次幂为 1。因此，该多项式的次数为 3。(ii) 在 $4 - y^2$ 中，常数项 4 的变量次幂为 0，$-y^2$ 的变量次幂为 2。因此，该多项式的次数为……阅读更多
待办事项：我们需要将下列多项式分类为一次、二次和三次多项式。解答：多项式是指每个项都是一个常数乘以一个变量的整数次幂的表达式。一次多项式是次数为 1 的多项式。二次多项式是次数为 2 的多项式。三次多项式是次数为 3 的多项式。多项式的次数是多项式中变量的最高次幂。因此，(i) 在 \( x^2 + x \) 中，$x^2$ 的变量次幂为 2。这意味着 \( x^2 + x \) 的次数为 2。因此，该多项式是二次多项式。(ii)……阅读更多
待办事项：我们需要求出多项式 \( 5x - 4x^2 + 3 \) 在以下情况下的值：(i) \( x = 0 \) (ii) \( x = -1 \) (iii) \( x = 2 \) 解答：为了求出多项式 $f(x)$ 在 $x = a$ 时的值，我们需要将 $x = a$ 代入 $f(x)$。设 $f(x) = 5x - 4x^2 + 3$。因此，(i) 当 $x = 0$ 时，$f(0) = 5(0) - 4(0)^2 + 3 = 0 - 4(0) + 3 = 0 - 0 + 3 = 3$。因此，多项式 \( 5x - 4x^2 + 3 \) 在 \( x = 0 \) 时的值为 3。(ii) 当 $x = -1$ 时，$f(-1) = 5(-1) - 4(-1)^2 + 3 = -5 - 4(1) + 3 = -5 - 4 + 3 = -6$。因此，多项式 \( 5x - 4x^2 + 3 \) 在 \( x = -1 \)……阅读更多