数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：一组学生在科学测试中获得的分数（满分 100 分）为 85、76、90、85、39、48、56、95、81 和 75。要求：我们必须找到：(i) 学生获得的最高分和最低分。(ii) 获得分数的范围。(iii) 该组学生的平均分。解答：学生获得的分数为 85, 76, 90, 85, 39, 48, 56, 95, 81, 75 (i) 学生获得的最高分 = 95 最低分 = 39 (ii) 获得分数的范围 = 最高分 - 最低分 = 95 - 39 = 56 (iii) 平均分 = 分数总和 / 分数个数… 阅读更多
已知：六年连续年份学校的招生人数如下：1555、1670、1750、2013、2540、2820 要求：我们必须找到该时期学校的平均招生人数。解答：平均数计算 平均招生人数 = 所有观测值的总和 / 观测值的个数 = (1555 + 1670 + 1750 + 2013 + 2540 + 2820) / 6 = 12348 / 6 = 2058 因此，该时期学校的平均招生人数为 2058。
某城市某周 7 天的降雨量（单位：毫米）记录如下：
| 日期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 降雨量（毫米） | 0.0 | 12.2 | 2.1 | 0.0 | 20.5 | 5.5 | 1.0 |
(i). 求上述数据的降雨量范围。
(ii). 求该周的平均降雨量。
(iii). 有多少天的降雨量小于平均降雨量？
已知：记录了某城市某周 7 天的降雨量（单位：毫米）。要求：我们必须 (i) 求上述数据的降雨量范围。(ii) 求该周的平均降雨量。(iii) 求有多少天的降雨量小于平均降雨量。解答：(i) 降雨量最高值（毫米）= 20.5 降雨量最低值（毫米）= 0.0 降雨量范围 = 最高降雨量 - 最低降雨量 = 20.5 - 0.0 = 20.5 毫米 (ii) 总天数 = 7 降雨量记录（毫米）= 0.0、12.2、2.1、0.0、20.5、5.5、1.0 平均降雨量（毫米）= 降雨量总和 / 天数… 阅读更多
已知：测量了 10 个女孩的身高（单位：厘米）。要求：我们必须回答给定的问题。解答：让我们将给定数据按升序排列：128、132、135、139、141、143、146、149、150、151 (i) 最高女孩的身高 = 151 厘米 (ii) 最矮女孩的身高 = 128 厘米 (iii) 范围 = 最高身高 - 最矮身高 = (151 - 128) = 23 厘米 (iv) 平均值 = 所有观测值的总和 / 观测值的总数 = 1414 / 10 = 141.4 厘米 (v) 身高高于平均身高的女孩人数 = 5
要求：我们必须判断给定的陈述是否正确。解答：(i) 我们知道众数是在给定数据中出现次数最多的观察值。因此，它是数据中的一个观察值。该陈述是正确的。(ii) 平均数可能是也可能不是数据中存在的数字之一。它也可以是一个不属于给定观察值的数据。该陈述是错误的。(iii) 中位数是给定数据在按升序或降序排列时的中间观察值。该陈述是正确的。(iv) 给定的数据… 阅读更多
要求：我们必须找到数据 13、16、12、14、19、12、14、13、14 的众数和中位数。解答：给定数据为：13、16、12、14、19、12、14、13、14。将数据按升序排列，我们得到：12、12、13、13、14、14、14、16、19。我们知道，给定数据的众数是指出现次数最多的观察值。14 在给定数据中出现三次。因此，众数 = 14 我们还知道，中位数是按升序排列的数据的中间观察值。在给定的 9 个观察值中，中间数据是第 5 个值。因此，中位数 = 14
已知：一个班 15 个学生的体重（公斤）为：38、42、35、37、45、50、32、43、43、40、36、38、43、38、47 要求：我们必须找到：(i) 该数据的众数和中位数。(ii) 是否存在多个众数。解答：学生总数 = 15 15 个学生的体重 = 38、42、35、37、45、50、32、43、43、40、36、38、43、38、47 按升序排列，我们得到：32、35、36、37、38、38、38、40、42、43、43、43、45、47、50 (i) 众数是在数据中出现次数最多的观察值。因此，… 阅读更多
已知：11 名球员在一场板球比赛中获得的分数如下：6、15、120、50、100、80、10、15、8、10、15 要求：我们必须找到该数据的平均数、众数和中位数，以及这三个数是否相同。解答：球员总数 = 11 球员得分 = 6、15、120、50、100、80、10、15、8、10、15 将得分按升序排列，我们得到 6、8、10、15、15、15、50、80、100、120 $\boxed{ \text { 平均数 }=\frac{ \text { 所有分数的总和 }}{ \text { 球员总数 }}}$ = (6 + 8 + 10 + 15 + 15 + 15 + 50 + 80 + 100 + 120) / 11 = 429 / 11 = 39 因此，平均数 = 39 众数是数据中出现… 阅读更多
已知：学生数学测试分数（满分 25 分）如下：19、25、23、20、9、20、15、10、5、16、25、20、24、12、20 要求：我们必须找到给定数据的众数和中位数。解答：将数据按升序排列，5、9、10、12、15、16、19、20、20、20、20、23、24、25、25 众数 = 最频繁的数据 众数 = 20 (20 在给定数据中出现 4 次) 中位数 = (n+1)/2 项，其中 n 为奇数。观测值数 n = 15 中位数 = (15 + 1)/2 项 = 16/2 项 = 第 8 项 第 8 项是 20。因此，中位数 = 20 众数和中位数的值相同 (20)。
"
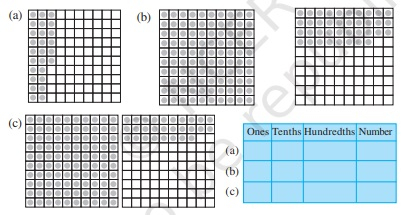
要求：我们必须借助方框完成表格，并用小数表示数字。解答：个位十分位百分位数字0260.261381.381281.28