数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究
"
压力与受力面积成反比。当砖块以 (A) 位置放置在桌子上时，接触面积最小，对桌子的压力最大。因此，选项 (a) 正确。
两个物体相互排斥，可能是因为它们带同种电荷而产生静电力，或者因为它们具有相同的磁极而产生磁力。因此，选项 (c) 正确。
只有当两个物体的表面接触时，才会产生摩擦力。因此，摩擦力是接触力。因此，选项 (b) 正确。
"
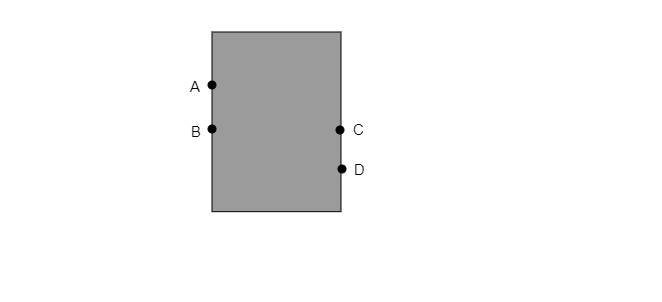
由于 B 和 C 水龙头在同一水平面上，因此水从 B 水龙头和 C 水龙头流出的压力相同。因为压力取决于重力、密度和高度。此处，重力和密度相同。因此，压力将取决于高度。此处 B 和 C 水龙头处于相同高度。因此，选项 (a) 正确。
在干燥的天气里，梳头时，有时我们会看到头发分开飞起来。这是因为梳头时头发和梳子带上了相反的电荷，从而产生了静电力。因此，选项 (b) 正确。
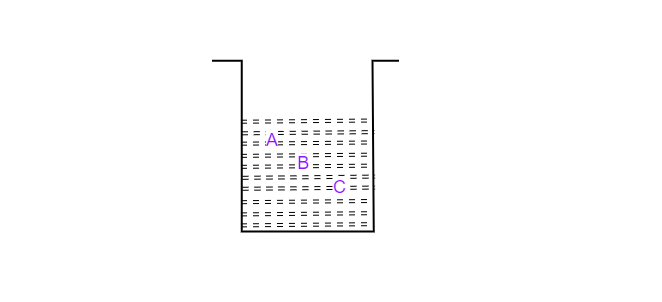
我们知道，液体中的压力随着深度的增加而增加。此处，B 点的深度大于 A 点，C 点的深度大于 A 点和 B 点。因此，A 点压力 < B 点压力 < C 点压力。因此，选项 (d) 正确。
已知：\( \left[\frac{\sin ^{2} 22^{\circ}+\sin ^{2} 68^{\circ}}{\cos ^{2} 22^{\circ}+\cos ^{2} 68^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \sin 27^{\circ}\right] \) 求解：我们需要求表达式 \( \left[\frac{\sin ^{2} 22^{\circ}+\sin ^{2} 68^{\circ}}{\cos ^{2} 22^{\circ}+\cos ^{2} 68^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \sin 27^{\circ}\right] \) 的值。解：我们知道，$\sin \left(90^{\circ}-\theta\right)=\cos \theta$，$\cos \left(90^{\circ}-\theta\right)=\sin \theta$，$\sin ^{2} \theta+\cos ^{2} \theta=1$。因此，$[\frac{\sin ^{2} 22^{\circ}+\sin ^{2} 68^{\circ}}{\cos ^{2} 22^{\circ}+\cos ^{2} 68^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \sin 27^{\circ}]=\frac{\sin ^{2} 22^{\circ}+\sin ^{2}(90^{\circ}-22^{\circ})}{\cos ^{2}(90^{\circ}-68^{\circ})+\cos ^{2} 68^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \sin (90^{\circ}-63^{\circ})$ $=\frac{\sin ^{2} 22^{\circ}+\cos ^{2} 22^{\circ}}{\sin ^{2} 68^{\circ}+\cos ^{2} 68^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \cos 63^{\circ}$$=\frac{1}{1}+(\sin ^{2} 63^{\circ}+\cos ^{2} 63^{\circ})$ $=1+1=2$ 阅读更多
已知：\( 4 \tan \theta=3 \) 求解：我们需要求 \( \left(\frac{4 \sin \theta-\cos \theta}{4 \sin \theta+\cos \theta}\right) \) 的值。解：$4 \tan \theta=3$，$\tan \theta=\frac{3}{4}$。因此，$\frac{4 \sin \theta-\cos \theta}{4 \sin \theta+\cos \theta}$。将分子和分母都除以 $\cos \theta$，我们得到，$\frac{4 \sin \theta-\cos \theta}{4 \sin \theta+\cos \theta}=\frac{4 \frac{\sin \theta}{\cos \theta}-1}{4 \frac{\sin \theta}{\cos \theta}+1}$$=\frac{4 \tan \theta-1}{4 \tan \theta+1}$ [因为 $\tan \theta=\frac{\sin \theta}{\cos \theta}$]$=\frac{4(\frac{3}{4})-1}{4(\frac{3}{4})+1}$ ($\tan \theta=\frac{3}{4}$)$=\frac{3-1}{3+1}$$=\frac{2}{4}$$=\frac{1}{2}$
已知：\( \sin \theta-\cos \theta=0 \) 求解：我们需要求 \( \left(\sin ^{4} \theta+\cos ^{4} \theta\right) \) 的值。解：我们知道，$\tan \theta=\frac{\sin \theta}{\cos \theta}$，$\tan 45^{\circ}=1$。因此，$\sin \theta-\cos \theta=0$，$\sin \theta=\cos \theta$，$\frac{\sin \theta}{\cos \theta}=1$，$\tan \theta=1$，$\tan \theta=\tan 45^{\circ}$，$\Rightarrow \theta=45^{\circ}$。这意味着，$\sin ^{4} \theta+\cos ^{4} \theta=\sin ^{4} 45^{\circ}+\cos ^{4} 45^{\circ}$$=(\frac{1}{\sqrt{2}})^{4}+(\frac{1}{\sqrt{2}})^{4}$ (因为 $\sin 45^{\circ}=\cos 45^{\circ}=\frac{1}{\sqrt{2}}$)$=\frac{1}{4}+\frac{1}{4}$$=\frac{2}{4}$$=\frac{1}{2}$
已知：\( \sin \left(45^{\circ}+\theta\right)-\cos \left(45^{\circ}-\theta\right) \) 求解：我们需要求 \( \sin \left(45^{\circ}+\theta\right)-\cos \left(45^{\circ}-\theta\right) \) 的值。解：我们知道，$\cos(90^o - \theta) = \sin \theta$。因此，$\sin (45^{\circ}+\theta)-\cos (45^{\circ}-\theta)= \cos[90^o- (45^o + \theta)] - \cos(45^o- \theta)$$= \cos (45^o - \theta) - \cos (45^o - \theta)$$= 0$