正确答案:解释:所有酯都具有羧基的共同结构,该结构由(d)中的后缀表示。
正确答案:(a) 加成反应 解释:油是不饱和化合物,含有双键。加成反应是不饱和烃的特征性质。
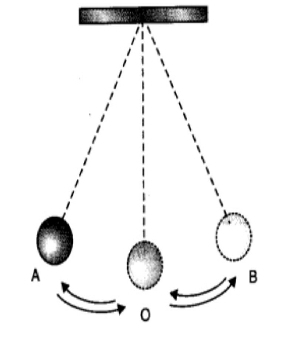
振荡次数 = 20 所需时间 t = 42 s 频率 f = 振荡次数 / 时间 = 20 / 42 s 所以,周期 T = 1 / f = 1 / (20/42) = 42/20 s = 2.1 s 因此,给定单摆的周期为 2.1 s。
正确答案:(a) (i) 和 (iv) 解释:无机酸是强酸,几乎完全电离;而羧酸是弱酸,仅部分电离。
通过观察给定的单摆图,我们发现单摆的周期是指它从 A 点运动到 B 点再返回 A 点所需的时间。
求解:我们需要求出给定数字的立方根。解:(i) $ \sqrt[3]{8 \times 125}=\sqrt[3]{2 \times 2 \times 2 \times 5 \times 5 \times 5}$$=\sqrt[3]{2^{3} \times 5^{3}}$$=2 \times 5$$=10$(ii) $\sqrt[3]{-1728 \times 216}=-\sqrt[3]{1728 \times 216}$$=-\sqrt[3]{1728} \times \sqrt[3]{216}$$=-\sqrt[3]{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3} \times \sqrt[3]{2 \times 2 \times 2 \times 3 \times 3 \times 3}$$=-\sqrt[3]{2^{3} \times 2^{3} \times 3^{3}} \times \sqrt[3]{2^{3} \times 3^{3}}$$=-(2 \times 2 \times 3) \times(2 \times 3)$$=-12 \times 6$$=-72$(iii) $\sqrt[3]{-27 \times 2744}=-\sqrt[3]{27 \times 2744}$$=-\sqrt[3]{27} \times \sqrt[3]{2744}$$=-(\sqrt[3]{3 \times 3 \times 3}) \times(\sqrt[3]{2 \times 2 \times 2 \times 7 ... 阅读更多
求解:我们需要计算 (i) \( \sqrt[3]{4^{3} \times 6^{3}} \) (ii) \( \sqrt[3]{8 \times 17 \times 17 \times 17} \) (iii) \( \sqrt[3]{700 \times 2 \times 49 \times 5} \) (iv) \( 125 \sqrt[3]{a^{6}}-\sqrt[3]{125 a^{6}} \) 解:(i) $\sqrt[3]{4^{3} \times 6^{3}}=\sqrt[3]{4^{3}}\times\sqrt[3]{6^{3}}$$=4 \times 6$$=24$(ii) $\sqrt[3]{8 \times 17 \times 17 \times 17}=\sqrt[3]{2 \times 2 \times 2 \times 17 \times 17 \times 17}$$=\sqrt[3]{2^{3} \times 17^{3}}$$=2 \times 17$$=34$(iii) $\sqrt[3]{700 \times 2 \times 49 \times 5}=\sqrt[3]{2 \times 2 \times 5 \times 5 \times 7 \times 2 \times 7 \times 7 \times 5}$$=\sqrt[3]{2^{3} \times 5^{3} \times 7^{3}}$$=2 \times 5 \times 7$$=70$(iv) $125\sqrt[3]{a^{6}}-\sqrt[3]{125 a^{6}}=125 \sqrt[3]{a^{2} \times a^{2} \times a^{2}}-\sqrt[3]{5 \times 5 \times 5 \times a^{2} \times a^{2} \times a^{2}}$$=125 \sqrt[3]{(a^{2})^{3}}-\sqrt[3]{5^{3} \times(a^{2})^{3}}$$=125 a^{2}-5 a^{2}$$=120 a^{2}$
求解:我们需要求出给定分数的立方根。解:(i) $\sqrt[3]{\frac{-125}{729}} =\frac{\sqrt[3]{-125}}{\sqrt[3]{729}}$$=\frac{-\sqrt[3]{125}}{\sqrt[3]{729}}$$=\frac{-\sqrt[3]{5 \times 5 \times 5}}{\sqrt[3]{3 \times 3 \times 3 \times 3 \times 3 \times 3}}$$=\frac{-\sqrt[3]{5^{3}}}{\sqrt[3]{3^{3} \times 3^{3}}}$$=\frac{-5}{3 \times 3}$$=\frac{-5}{9}$(ii) $\sqrt[3]{\frac{10648}{12167}}=\frac{\sqrt[3]{10648}}{\sqrt[3]{12167}}$$=\frac{\sqrt[3]{2 \times 2 \times 2 \times 11 \times 11 \times 11}}{\sqrt[3]{23 \times 23 \times 23}}$$=\frac{\sqrt[3]{2^{3} \times 11^{3}}}{\sqrt[3]{23^{3}}}$$=\frac{2 \times 11}{23}$$=\frac{22}{23}$(iii) $\sqrt[3]{\frac{-19683}{24389}}=\frac{\sqrt[3]{-19683}}{\sqrt[3]{24389}}$$=\frac{-\sqrt[3]{19683}}{\sqrt[3]{24389}}$$=\frac{-\sqrt[3]{3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3}}{\sqrt[3]{29 \times 29 \times 29}}$$=\frac{-\sqrt[3]{3^{3} \times 3^{3} \times 3^{3}}}{\sqrt[3]{29^{3}}}$$=\frac{-(3 \times 3 \times 3)}{29}$$=\frac{-27}{29}$(iv) $\sqrt[3]{\frac{686}{-3456}}=\sqrt[3]{\frac{2 \times 343}{-2 \times 1728}}$$=\sqrt[3]{\frac{343}{-1728}}$$=\frac{\sqrt[3]{343}}{\sqrt[3]{-1728}}$$=\frac{\sqrt[3]{343}}{-\sqrt[3]{1728}}$$=\frac{\sqrt[3]{7 \times 7 \times 7}}{-\sqrt[3]{2 \times 2 \times 2 \times 2 \times 2 \times ... 阅读更多
求解:我们需要求出给定分数的立方根。解:(i) $\sqrt[3]{0.001728}=\sqrt[3]{\frac{1728}{1000000}}$$=\frac{\sqrt[3]{1728}}{\sqrt[3]{1000000}}$$=\frac{\sqrt[3]{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3}}{\sqrt[3]{10 \times 10 \times 10 \times 10 \times 10 \times 10}}$$=\frac{\sqrt[3]{2^{3} \times 2^{3} \times 3^{3}}}{\sqrt[3]{10^{3} \times 10^{3}}}$$=\frac{2 \times 2 \times 3}{10 \times 10}$$=\frac{12}{100}$$=0.12$(ii) $\sqrt[3]{0.003375}=\sqrt[3]{\frac{3375}{1000000}}$$=\frac{\sqrt[3]{3375}}{\sqrt[3]{1000000}}$$=\frac{\sqrt[3]{3 \times 3 \times 3 \times 5 \times 5 \times 5}}{\sqrt[3]{10 \times 10 \times 10 \times 10 \times 10 \times 10}}$$=\frac{\sqrt[3]{3^{3} \times 5^{3}}}{\sqrt[3]{10^{3} \times 10^{3}}}$$=\frac{3 \times 5}{10 \times 10}$$=\frac{15}{100}$$=0.15$(iii) $\sqrt[3]{0.001}=\sqrt[3]{\frac{1}{1000}}$$=\frac{\sqrt[3]{1}}{\sqrt[3]{1000}}$$=\frac{\sqrt[3]{1 \times 1 \times 1}}{\sqrt[3]{10 \times 10 \times 10}}$$=\frac{1}{\sqrt[3]{10^{3}}}$$=\frac{1}{10}$$=0.1$(iv) $\sqrt[3]{1.331}=\sqrt[3]{\frac{1331}{1000}}$$=\frac{\sqrt[3]{1331}}{\sqrt[3]{1000}}$$=\frac{\sqrt[3]{11 \times 11 \times 11}}{\sqrt[3]{10 \times 10 \times 10}}$$=\frac{\sqrt[3]{11^{3}}}{\sqrt[3]{10^{3}}}$$=\frac{11}{10}$$=1.1$阅读更多
求解:我们需要计算以下表达式。解:(i) $\sqrt[3]{27}+\sqrt[3]{0.008}+\sqrt[3]{0.064}= \sqrt[3]{3 \times 3 \times 3}+\sqrt[3]{\frac{8}{1000}}+\sqrt[3]{\frac{64}{1000}}$$=\sqrt[3]{3^{3}}+\sqrt[3]{\frac{2 \times 2 \times 2}{10 \times 10 \times 10}}+\sqrt[3]{\frac{4 \times 4 \times 4}{10 \times 10 \times 10}}$$=3+\frac{2}{10}+\frac{4}{10}$$=3+0.2+0.4$$=3.6$(ii) $\sqrt[3]{1000}+\sqrt[3]{0.008}-\sqrt[3]{0.125}=\sqrt[3]{10 \times 10 \times 10}+\sqrt[3]{\frac{8}{1000}}-\sqrt[3]{\frac{125}{1000}}$$=\sqrt[3]{10^{3}}+\sqrt[3]{\frac{2 \times 2 \times 2}{10 \times 10 \times 10}}-\sqrt[3]{\frac{5 \times 5 \times 5}{10 \times 10 \times 10}}$$=\sqrt[3]{10^{3}}+\sqrt[3]{\frac{2^{3}}{10^{3}}}-\sqrt[3]{\frac{5^{3}}{10^{3}}}$$=10+\frac{2}{10}-\frac{5}{10}$$=10+0.2-0.5$$=10.2-0.5$$=9.7$(iii) $\sqrt[3]{\frac{729}{216}} \times \frac{6}{9}=\frac{\sqrt[3]{729}}{\sqrt[3]{216}} \times \frac{6}{9}$$=\frac{\sqrt[3]{9 \times 9 \times 9}}{\sqrt[3]{6 \times 6 \times 6}} \times \frac{6}{9}$$=\frac{\sqrt[3]{9^{3}}}{\sqrt[3]{6^{3}}} \times \frac{6}{9}$$=\frac{9}{6} \times \frac{6}{9}$$=1$(iv) $\sqrt[3]{\frac{0.027}{0.008}} \div \sqrt{\frac{0.09}{0.04}}-1=\frac{\sqrt[3]{0.027}}{\sqrt[3]{0.008}} \div \sqrt{\frac{0.09}{0.04}}-1$$=\frac{\sqrt[3]{\frac{27}{1000}}}{\sqrt[3]{\frac{8}{1000}}} \div \frac{\sqrt{\frac{9}{100}}}{\sqrt{\frac{4}{100}}}-1$$=\frac{\sqrt[3]{\frac{27}{1000}}}{\sqrt[3]{\frac{8}{1000}}} \div \frac{\sqrt{\frac{9}{100}}}{\sqrt{\frac{4}{100}}} -1$$=\frac{\frac{\sqrt[3]{27}}{\sqrt[3]{1000}}}{\frac{\sqrt[3]{8}}{\sqrt[3]{1000}}} \div \frac{\frac{\sqrt{9}}{\sqrt{100}}}{\frac{\sqrt{4}}{\sqrt{100}}} -1$$=\frac{\frac{\sqrt[3]{3^{3}}}{\sqrt[3]{10^{3}}}}{\frac{\sqrt[3]{2^{3}}}{\sqrt[3]{10^{3}}}} \div \frac{\frac{\sqrt{3^{2}}}{\sqrt{10^{2}}}}{\frac{\sqrt{2^{2}}}{\sqrt{10^{2}}}} -1$$=\frac{\frac{3}{10}}{\frac{2}{10}} \div \frac{\frac{3}{10}}{\frac{2}{10}} -1$$=\frac{3}{2} \times \frac{2}{3}-1$$=1-1$$=0$(v) $\sqrt[3]{0.1 \times 0.1 \times 0.1 \times 13 \times 13 ... 阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP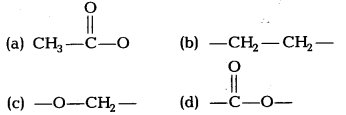

 "\
"\