(i) 溴乙烷 (ii) 甲醛 (iii) 1-己炔。
(i) 乙酸 (CH3COOH) (ii) 溴戊烷 (C5H11Br) (iii) 丁酮 (CH3 — CH2 — COCH3) (iv) 己醛 (C5H11CHO)
环戊烷的分子式为 C5 H10。
已知:一个半径为 $20\ m$ 的圆形公园位于一个小区内。三个男孩安库尔、阿米特和阿南德坐在它的边界上等距的位置,每个人手里都拿着一个玩具电话互相交谈。求解:我们需要找到每部电话线的长度。解答:圆形公园的半径 $= 20\ m$安库尔、阿米特和阿南德彼此等距。连接这些点,形成一个等边三角形 $ABC$。将 $BO$ 延长到 $L$,它是 $AC$ 的垂直平分线。因此,$BL = 20 + 10$$= 30\ m$ ... 阅读更多
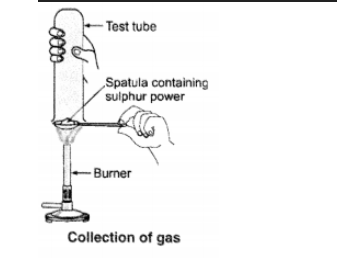
普拉蒂尤什用药勺取一些硫磺粉末并加热它。他通过将试管倒置在上面来收集产生的气体,如图所示。
(a) 气体对
(i) 干石蕊试纸有什么作用?
(ii) 湿石蕊试纸有什么作用?
写出发生反应的平衡化学方程式。
 "\
"\
(i) 干石蕊试纸 – 没有作用。(ii) 湿石蕊试纸 – 变红。[额外信息:石蕊是一种天然指示剂。天然指示剂是一种天然存在的指示剂,可以帮助我们知道被测试的物质是酸性物质还是碱性物质。它来源于地衣。获得石蕊溶液的过程需要压碎和研磨地衣。除石蕊外,其他一些天然指示剂包括:红甘蓝、姜黄、芜菁皮、咖喱粉等。用途:它用于测试物质的酸度和碱度。这种溶液还可以… 阅读更多
已知:3600 求解:我们需要找到最小的数,用它乘以 3600 后,其乘积是一个完全立方数,并求出该乘积的立方根。解答:3600 的质因数分解为:$3600=2\times2\times2\times2\times3\times3\times5\times5$$=2^3\times2\times3^2\times5^2$将因子分组为相等因子的三元组,我们看到剩下 $2, 3^2$ 和 $5^2$。为了使 3600 成为一个完全立方数,我们必须用 $2^2\times3\times5=60$ 乘以它。$3600\times60=2^3\times2\times3^2\times5^2\times2^2\times3\times5$$=2^3\times2^3\times3^3\times5^3$$\sqrt[3]{216000}=\sqrt[3]{2^3\times2^3\times3^3\times5^3}$$=2\times2\times3\times5$$=60$必须将 3600 乘以最小的数 60,才能使其乘积成为一个完全立方数,并且该乘积的立方根是 60。阅读更多
已知:210125 求解:我们需要找到最小的数,用它乘以 210125 后,其乘积是一个完全立方数,并求出该乘积的立方根。解答:210125 的质因数分解为:$210125=5\times5\times5\times41\times41$$=5^3\times41^2$将因子分组为相等因子的三元组,我们看到剩下 $41^2$。为了使 210125 成为一个完全立方数,我们必须用 41 乘以它。$210125\times41=5^3\times41^2\times41$$=5^3\times41^3$$\sqrt[3]{8615125}=\sqrt[3]{5^3\times41^3}$$=5\times41$$=205$必须将 210125 乘以最小的数 41,才能使其乘积成为一个完全立方数,并且该乘积的立方根是 205。阅读更多
已知:210125 求解:我们需要找到最小的数,用它去除 8192 后,其商是一个完全立方数,并求出该商的立方根。解答:8192 的质因数分解为:$8192=2\times2\times2\times2\times2\times2\times2\times2\times2\times2\times2\times2\times2$$=2^3\times2^3\times2^3\times2^3\times2$将因子分组为相等因子的三元组,我们看到剩下 2。为了使 8192 成为一个完全立方数,我们必须用 2 除以它。$8192\div2=2\times2\times2\times2\times2\times2\times2\times2\times2\times2\times2\times2\times2\div2$$=2^3\times2^3\times2^3\times2^3\times2\div2$$\sqrt[3]{4096}=\sqrt[3]{2^3\times2^3\times2^3\times2^3}$$=2\times2\times2\times2$$=16$必须用最小的数 2 除以 8192,才能使其商为一个完全立方数,并且该商的立方根是 16。阅读更多
已知:三个数的比例为 $1:2:3$,它们的立方和为 $98784$。求解:我们需要找到这些数。解答:设第一个数为 $x$。这意味着,第二个数是 $2x$。第三个数是 $3x$。根据题意,它们的立方和为 $98784$。$\Rightarrow x^3+( 2x)^3+( 3x)^3=98784$$\Rightarrow x^3+8x^3+27x^3=98784$$\Rightarrow 36x^3=98784$$\Rightarrow x^3=\frac{98784}{36}$$\Rightarrow x^3=2744$$\Rightarrow x=\sqrt[3]{2744}$$\Rightarrow x=\sqrt[3]{2\times2\times2\times7\times7\times7}$$\Rightarrow x=2\times7=14$因此,第一个数 $=x=14$第二个数 $=2x=2\times14=28$第三个数 $=3x=3\times14=42$因此,这三个数是 $14, \ 28$ 和 $42$。阅读更多
因此,立方体的边长为 210 m。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP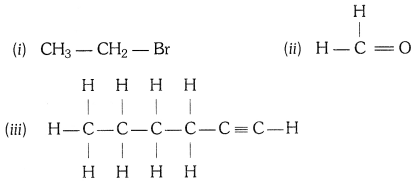 \
\