在一个小区里，有一个半径为20米的圆形公园。三个男孩安库尔、赛义德和戴维德坐在公园边界上等距离的位置，每个人手里都拿着一个玩具电话，以便互相通话。求每个电话线的长度。

已知

一个半径为 $20\ m$ 的圆形公园位于一个小区内。三个男孩安库尔、阿米特和阿南德坐在其边界上等距离的位置，每个人手里都拿着一个玩具电话，以便互相通话。

要求

我们必须找到每部电话线的长度。

解答

圆形公园的半径 $= 20\ m$

安库尔、阿米特和阿南德彼此之间等距。

连接这些点，形成一个等边三角形 $ABC$。

延长 $BO$ 到 $L$，它是 $AC$ 的垂直平分线。

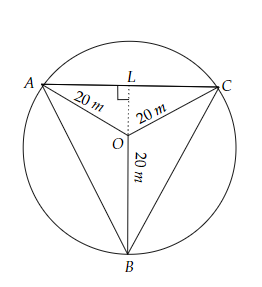
因此，

$BL = 20 + 10$

$= 30\ m$              ($O$ 是 $\triangle ABC$ 的重心)

设 $a$ 为 $\triangle ABC$ 的边长

$\Rightarrow \frac{\sqrt{3}}{2} a=30$

$a=\frac{30 \times 2}{\sqrt{3}}$

$a=\frac{60 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}$

$a=\frac{60 \times \sqrt{3}}{3}$

$a=20 \sqrt{3} \mathrm{~m}$

因此，他们彼此之间的距离为 $20\sqrt3\ m$。 

Tutorialspoint

更新于: 2022年10月10日

200 次浏览

开启您的 职业生涯

通过完成课程获得认证

开始学习