数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究
已知：给定的有理数为$\frac{1}{5}$和$\frac{1}{2}$。要做：我们必须在$\frac{1}{5}$和$\frac{1}{2}$之间找到两个有理数。解：5和2的最小公倍数是10。$\frac{1}{5}$可以写成$\frac{1}{5}=\frac{1\times2}{5\times2}$$=\frac{2}{10}$$\frac{1}{2}=\frac{1\times5}{2\times5}$$=\frac{5}{10}$$\frac{3}{10}$和$\frac{4}{10}$位于$\frac{2}{10}$和$\frac{5}{10}$之间。因此，在$\frac{1}{5}$和$\frac{1}{2}$之间的两个有理数是$\frac{3}{10}$，$\frac{4}{10}$。
已知：给定的有理数为$\frac{1}{4}$和$\frac{1}{2}$。要做：我们必须在$\frac{1}{4}$和$\frac{1}{2}$之间找到十个有理数。解：4和2的最小公倍数是4。$\frac{1}{2}=\frac{1\times2}{2\times2}$$=\frac{2}{4}$因为我们需要在$\frac{1}{4}$和$\frac{2}{4}$之间找到10个有理数，所以将两个分数都乘以$\frac{20}{20}$。这意味着，$\frac{1}{4}=\frac{1}{4}\times\frac{20}{20}$$=\frac{20}{80}$$\frac{2}{4}=\frac{2}{4}\times\frac{20}{20}$$=\frac{40}{80}$这意味着，$\frac{21}{80}$，$\frac{22}{80}$，……，$\frac{38}{80}$，$\frac{39}{80}$位于$\frac{20}{80}$和$\frac{40}{80}$之间。因此，在$\frac{1}{4}$和$\frac{1}{2}$之间的十个有理数是$\frac{21}{80}$，$\frac{22}{80}$，……，$\frac{38}{80}$，$\frac{39}{80}$。
已知：给定的有理数为$\frac{-2}{5}$和$\frac{1}{2}$。要做：我们必须在$\frac{-2}{5}$和$\frac{1}{2}$之间找到十个有理数。解：5和2的最小公倍数是10。$\frac{-2}{5}=\frac{-2\times2}{5\times2}$$=\frac{-4}{10}$$\frac{1}{2}=\frac{1\times5}{2\times5}$$=\frac{5}{10}$因为我们需要在$\frac{-4}{10}$和$\frac{5}{10}$之间找到10个有理数，所以将两个分数都乘以$\frac{2}{2}$。这意味着，$\frac{-4}{10}=\frac{-4}{10}\times\frac{2}{2}$$=\frac{-8}{20}$$\frac{5}{10}=\frac{5}{10}\times\frac{2}{2}$$=\frac{10}{20}$因此，在$\frac{-2}{5}$和$\frac{1}{2}$之间的十个有理数是$\frac{-7}{20}$，$\frac{-6}{20}$，……，$\frac{1}{20}$，$\frac{2}{20}$。
要做：我们必须将每个给定的有理数表示为$\frac{p}{q}$的形式。解：我们知道，$a^{-m}=\frac{1}{a^m}$$a^{m}=\frac{1}{a^{-m}}$ 因此，(i)$2^{-3}=\frac{1}{2^3}$$=\frac{1}{8}$(ii) $(-4)^{-2}=\frac{1}{(-4)^2}$$=\frac{1}{16}$ (iii) $\frac{1}{3^{-2}}=3^2$$=9$(iv)$\frac{1}{2^{-5}}=2^5$$=32$ (v) $(\frac{2}{3})^{-2}=\frac{1}{(\frac{2}{3})^{2}}$$=(\frac{3}{2})^{2}$ $=\frac{3^2}{2^2}$$=\frac{9}{4}$
要做：我们必须求每个给定表达式的值。解：我们知道，$a^{-m}=\frac{1}{a^{m}}$$a^o=1$因此，(i) $3^{-1}+4^{-1}=\frac{1}{3}+\frac{1}{4}$$=\frac{1\times4+1\times3}{12}$ (3和4的最小公倍数是12)$=\frac{4+3}{12}$$=\frac{7}{12}$(ii) $(3^{0}+4^{-1}) \times 2^{2}=(1+\frac{1}{4})\times4$$=\frac{1\times4+1}{4}\times4$$=\frac{5}{4}\times4$$=5$(iii) $(3^{-1}+4^{-1}+5^{-1})^{0}=(\frac{1}{3}+\frac{1}{4}+\frac{1}{5})^o$$=1$(iv) $[{(\frac{1}{3})^{-1}-(\frac{1}{4})^{-1}}]^{-1} =[{(3)^{1}-(4)^{1}}]^{-1}$$=(3-4)^{-1}$$=(-1)^{-1}$$=\frac{1}{(-1)^{1}}$$=\frac{1}{-1}$$=-1$
要做：我们必须求每个给定表达式的值。解：我们知道，$a^{-m}=\frac{1}{a^{m}}$因此，(i) $(\frac{1}{2})^{-1}+(\frac{1}{3})^{-1}+(\frac{1}{4})^{-1}=(2)^{1}+(3)^{1}+(4)^{1}$$=2+3+4$$=9$(ii) $(\frac{1}{2})^{-2}+(\frac{1}{3})^{-2}+(\frac{1}{4})^{-2}=(2)^{2}+(3)^{2}+(4)^{2}$$=4+9+16$$=29$(iii) $(2^{-1} \times 4^{-1}) \div 2^{-2}=(\frac{1}{2} \times \frac{1}{4}) \div \frac{1}{2^{2}}$$=\frac{1}{8} \div \frac{1}{4}$$=\frac{1}{8} \times \frac{4}{1}$$=\frac{1}{2}$(iv) $(5^{-1} \times 2^{-1}) \div 6^{-1}=(\frac{1}{5} \times \frac{1}{2}) \div \frac{1}{6}$$=\frac{1}{10} \times \frac{6}{1}$$=\frac{6}{10}$$=\frac{3}{5}$
火箭的工作原理是动量守恒定律。选项 (c) 正确。
这里，物体的质量$m=2\ kg$，运动物体的速度$v=4\ m/s$。由于速度不变，所以加速度为零。因此，所需的力$F=ma=2\ kg\times0=0$。所以，选项 (b) 正确。
使小型汽车比大型汽车更容易加速的物理量是质量，以 kg 为单位测量。所以，选项 (b) 正确。
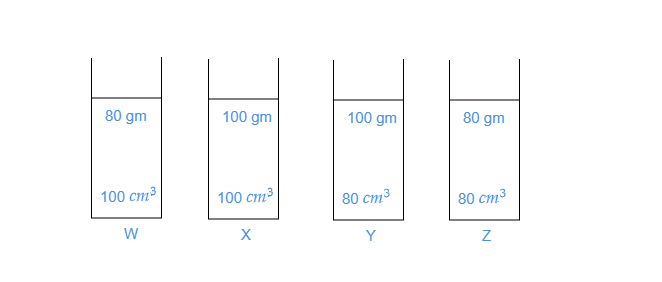
在容器 X 中：液体的密度$d_W=\frac{质量}{体积}$$=\frac{80\ gm}{100\ cm^3}$$=0.8\ gm/cm^3$在容器 X 中：液体的密度$d_X=\frac{质量}{体积}$$=\frac{100\ gm}{100\ cm^3}$$=1\ gm/cm^3$ 在容器 Y 中：液体的密度$d_Y=\frac{质量}{体积}$$=\frac{100\ gm}{80\ cm^3}$$=1.25\ gm/cm^3$在容器 Z 中：液体的密度$d_Z=\frac{质量}{体积}$$=\frac{80\ gm}{80\ cm^3}$$=1\ gm/cm^3$在这里我们观察到，$d_X=d_Z$，这意味着容器 X 和 Z 中液体的密度相同。因此可以说，容器 X 和容器 Z 中的液体可能含有相同的液体。所以，选项 (d) 正确。阅读更多