已知:$O$是圆心。$\angle APB = 50^o$。求解:我们需要求出$\angle AOB$和$\angle OAB$。解:弧$AB$在圆心处构成角$\angle AOB$,在圆的其余部分构成角$\angle APB$。这意味着,$\angle AOB = 2\angle APB = 2 \times 50^o = 100^o$连接$AB$。$\triangle AOB$是一个等腰三角形,其中$OA = OB$。因此,$\angle OAB = \angle OBA$ $\angle OAB + \angle OBA = 180^o - 100^o = 80^o$ $2\angle OAB = 80^o$ $\angle OAB =\frac{80^o}{2} = 40^o$。
已知:一个半径为$40\ m$的圆形公园位于一个小区内。三个男孩安库尔、阿米特和阿南德坐在其边界上等距的位置,每个人手中都拿着一个玩具电话互相交谈。求解:我们需要求出每个电话线的长度。解:圆形公园的半径$= 40\ m$安库尔、阿米特和阿南德彼此等距。连接这些点,形成一个等边三角形$ABC$。将$BO$延长至$L$,它是$AC$的垂直平分线。因此,$BL = 40 + 20 = 60\ m$ ... 阅读更多
方程\( x-y=10 \)和\( x+y=70 \)的解是\( \ldots \)
A) \( (40,30) \)
B) (30,40)
C) \( (10,60) \)
D) \( (50,20) \)
已知:给定的方程组是\( x-y=10 \)和\( x+y=70 \)。求解:我们需要求解这个方程组。解:将给定的方程相加,得到$(x-y)+(x+y)=10+70$ $x+x-y+y=80$ $2x=80$ $x=\frac{80}{2} = 40$将$x=40$代入$x+y=70$,得到$40+y=70$ $y=70-40=30$因此,给定方程组的解是$(40, 30)$。
燃料的热值是指完全燃烧1公斤燃料所产生的热量。60公斤燃料产生的热量 = 180000千焦。1公斤燃料产生的热量 = 180000/60 = 3000千焦/公斤。因此,该燃料的热值为3000千焦/公斤。
热值为20千焦/公斤。这意味着燃烧1公斤燃料会释放20千焦的热量。燃烧释放50千焦热量的燃料量为:(50千焦)/(20千焦/公斤) = 2.5公斤
一个家庭30天消耗12公斤液化石油气。那么,家庭每天消耗的液化石油气 = 12/30公斤 = 0.4公斤。液化石油气的热值 = 50焦耳/公斤(热值是特定数量燃料或食物产生的热量的度量。通常以焦耳/公斤表示。)每天平均消耗的能量 = 液化石油气的热值 × 每天消耗的液化石油气量 = 50 × 0.4焦耳 = 20焦耳因此,每天消耗20焦耳的能量。
两个物体之间的吸引力总是与其质量成正比。对于两个板球:板球的质量非常小,因此它们之间的万有引力非常小。对于一个板球和地球:由于地球的质量很大,因此板球和地球之间的万有引力非常大。
我们知道两个物体之间万有引力的公式。$F=G\frac{m_1m_2}{r^2}$ 其中,$F\rightarrow$万有引力 $G\rightarrow$万有引力常数 $m_1\rightarrow$第一个物体的质量 $m_2\rightarrow$第二个物体的质量 $r\rightarrow$两个物体之间的距离 如果我们将两个物体之间的距离加倍,则吸引力$F=G\frac{m_1m_2}{(2r)^2} = \frac{1}{4}\times G\frac{m_1m_2}{r^2}$ 因此,将两个物体之间的距离加倍,万有引力将变成原来的四分之一。如果我们将两个物体之间的距离减半,则万有引力为:$F=G\frac{m_1m_2}{(\frac{r}{2})^2}$ 或 $F=4\timesG\frac{m_1m_2}{r^2}$ 因此,如果两个物体之间的距离减半,则... 阅读更多
万有引力定律的应用。(i) 万有引力定律用于精确确定太阳、地球和月球的质量。(ii) 万有引力定律也用于发现宇宙中的新恒星和行星。
这里给出,物体的质量$m=150\ kg$ 地球的质量$M=6\times10^{24}\ kg$ 地球的半径$R=6.4\times10^{6}\ m$ 万有引力常数$G=6.7\times10^{-11}\ Nm^2kg^{-2}$ 因此,物体上的万有引力$F=G\frac{Mm}{R^2}$ 或 $F=6.7\times10^{-11}\ Nm^2kg^{-2}\times\frac{6\times10^{24}\times150}{(6.4\times10^{6})^2}$ 或 $F=1472.1\ N$ 因此,质量为$150\ kg$的物体在地球表面上的万有引力为$1472.1\ N$。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP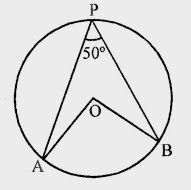 "\
"\