数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法学研究
已知：一个三角形最多不能超过……个钝角。需要：我们必须填入给定的空格。解答：根据三角形的角度和性质，三角形三个角的和为 180°。如果三角形中有两个或两个以上钝角，则三角形的角度和将超过 180°，这在三角形中是不可能的。因此，一个三角形最多不能超过一个钝角。
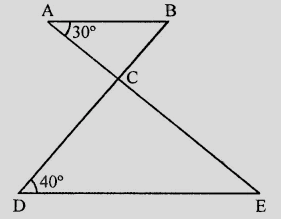
"\已知：在给定图形中，$AB \parallel DE$。需要：我们必须找到 $\angle ACD$。解答：$AE$ 和 $BD$ 相交于 $C$ $\angle BAC = 30^o$ 和 $\angle CDE = 40^o$ $AB \parallel DE$这意味着，$\angle ABC = \angle CDE$ (内错角)$\angle ABC = 40^o$在 $\triangle ABC$ 中，$BC$ 被延长 $\angle ACD = \angle CAB + \angle ABC$ $= 30^o + 40^o$ $= 70^o$ $\angle ACD$ 的值为 $70^o$。
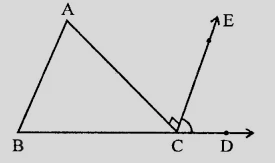
"\已知：在给定图形中，$AC \perp CE$ 且 $\angle A: \angle B : \angle C = 3:2:1$。需要：我们必须找到 $\angle ECD$ 的值。解答：我们知道，三角形中角度的和为 $180^o$。$\angle A + \angle B + \angle C = 180^o$设 $\angle A = 3x$这意味着，$\angle B = 2x$ 和 $\angle C = x$因此，$3x + 2x + x = 180^o$ $6x = 180^o$ $x = \frac{180^o}{6}$ $x = 30^o$这意味着，$\angle A = 3x = 3(30^o) = 90^o$ $\angle B = 2x = 2(30^o) = 60^o$ $\angle C = x = 30^o$在 $\triangle ABC$ 中，外角 $\angle ACD = ... 阅读更多
已知：\( x-\sqrt{3} \) 是多项式 \( p(x) = a x^{2}+b x-3 \) 的一个因式，并且 \( a+b=2-\sqrt{3} \)。需要：我们必须找到 \( a \) 和 \( b \) 的值。解答：$a+b=2-\sqrt{3}$.............(i)\( x-\sqrt{3} \) 是多项式 \( p(x) = a x^{2}+b x-3 \) 的一个因式这意味着，$p(\sqrt3)=a(\sqrt3)^2+b(\sqrt3)-3=0$$3a+\sqrt3b-3=0$$3a+\sqrt3b=3$$\sqrt3(\sqrt3a+b)=(\sqrt3)^2$$\sqrt3a+b=\sqrt3$.........(ii)从 (i) 中减去 (ii)，我们得到，$a+b-\sqrt3a-b=2-\sqrt3-\sqrt3$$a-\sqrt3a=2-2\sqrt3$$a(1-\sqrt3)=2(1-\sqrt3)$$a=2$这意味着，$2+b=2-\sqrt3$$b=-\sqrt3$阅读更多
PVC（聚氯乙烯）袋、塑料瓶和塑料椅子是由热塑性塑料制成的，因此可以回收利用。热塑性材料是由聚合物组成的，这些聚合物通过分子间力连接在一起，形成线形或支链结构。对于热塑性塑料，形状在冷却时会硬化，但在再次加热时可以重新成型。电话机、炊具手柄、电开关和圆珠笔是由热固性塑料制成的，因此不能回收利用。热固性塑料是指由化学键连接在一起的聚合物制成的材料，具有高度交联的聚合物结构。热固性聚合物一旦成型，就不能在…… 阅读更多
(a) 涤纶和 PET 是聚酯。聚酯是一种合成纤维，它含有与赋予水果甜味的物质相似的有机基团。它用于制造瓶子和餐具，从而替代了玻璃等材料。(b) 尼龙是一种聚酰胺。尼龙是第一种全合成纤维。它是用煤、水和空气制成的。(c) 丙烯酸纤维用作羊毛的替代品。它是一种看起来像羊毛的合成纤维。(d) PET 是一种用作玻璃替代品的材料。它是一种聚酯。聚酯是一种合成纤维，由…… 阅读更多
(i) 涤纶可能是含有大量酯基团的合成纤维 B。(ii) 人造丝可能是由含有葡萄糖的聚合物 D 制成的合成纤维 C。(iii) 尼龙可能是纤维 A，它在化学上是一种聚酰胺，是尼龙。它是第一种全合成纤维。它是用煤、水和空气制成的。(b) 聚合物 D 是纤维素。聚合物是由许多重复单元组成的。聚合物也存在于自然界中。例如，棉花是一种天然聚合物，由纤维素制成。纤维素是由大量的葡萄糖单元组成的。(c)…… 阅读更多
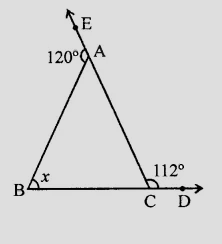
"\已知：在 $\triangle ABC$ 中，边 $BC$ 和 $CA$ 分别被延长到 $D$ 和 $E$。$\angle \mathrm{ACD}=112^{\circ}$ 和 $\angle \mathrm{BAE}=120^{\circ}$需要：我们必须计算 $x$ 的值。解答：$\angle \mathrm{ACB}+\angle \mathrm{ACD}=180^{\circ}$$\angle \mathrm{ACB}+112^{\circ}=180^{\circ}$$\angle \mathrm{ACB}=180^{\circ}-112^{\circ}=68^{\circ}$同样地，$\angle \mathrm{BAE}+\angle \mathrm{BAC}=180^{\circ}$$120^{\circ}+\angle \mathrm{BAC}=180^{\circ}$$\angle \mathrm{BAC}=180^{\circ}-120^{\circ}=60^{\circ}$$\angle \mathrm{BAC}+\angle \mathrm{ABC}+\angle \mathrm{BCA}=180^{\circ}$$60^{\circ}+x+68^{\circ}=180^{\circ}$$128^{\circ}+x=180^{\circ}$$x=180^{\circ}-128^{\circ}=52^{\circ}$因此，$x$ 的值为 $52^{\circ}$。阅读更多
已知：三角形的每个角都小于其他两个角的和。需要：我们必须证明该三角形是锐角三角形。解答：设在 $\triangle ABC$ 中，$\angle A < \angle B + \angle C$这意味着，$\angle A + \angle A < \angle A + \angle B + \angle C$$2\angle A < 180^o$$\angle A < 90^o$同样地，$\angle B < 90^o$ $\angle C < 90^o$因此，三角形的每个角都是锐角。
已知：三角形底边向两边延长所得的外角分别为104°和136°。求解：求三角形的所有角度。解：设三角形为ABC，底边BC分别向D和E延长，形成∠ABE = 104°和∠ACD = 136°。由图可知，∠ABC + ∠ABE = 180°∠ABC + 104° = 180°∠ABC = 180° - 104° = 76°同理，∠ACB + ∠ACD = 180°∠ACB + 136° = 180°∠ACB = 180° - 136° = 44°∠ABC + ∠ACB + ∠BAC = 180° (三角形内角和定理)76° + 44° + ∠BAC = 180°120° + ∠BAC = 180°∠BAC = 180° - 120° = 60°因此，三角形的角度分别为44°、60°和76°。阅读更多