如图所示，$AC \perp CE$ 且 $\angle A: \angle B : \angle C = 3:2:1$，求 $\angle ECD$ 的值。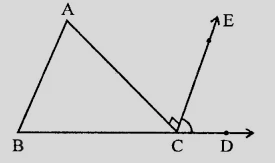"\n

已知

在给定图形中，$AC \perp CE$ 且 $\angle A: \angle B : \angle C = 3:2:1$。

要求

我们需要求 $\angle ECD$ 的值。

解答

我们知道，

三角形内角和为 $180^o$。

$\angle A + \angle B + \angle C = 180^o$

$\angle A = 3x$

假设

$\angle B = 2x$ 和 $\angle C = x$

因此，

$3x + 2x + x = 180^o$

$6x = 180^o$

$x = \frac{180^o}{6}$

$x = 30^o$

假设

$\angle A = 3x = 3(30^o) = 90^o$

$\angle B = 2x = 2(30^o) = 60^o$

$\angle C = x = 30^o$

在 $\triangle ABC$ 中，

外角 $\angle ACD = \angle A + \angle B$

$90^o + \angle ECD = 90^o + 60^o = 150^o$

$\angle ECD = 150^o-90^o = 60^o$

$\angle ECD$ 的值为 $60^o$。

教程点

更新于: 2022年10月10日

38 次浏览

开启你的 职业生涯

通过完成课程获得认证

立即开始