数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
这里，手是施力的主体，牙膏管是受力物体，牙膏从管中挤出是施力产生的结果。
通过放射性物质的衰变或放射性原子核的衰变，可以产生伽马射线。
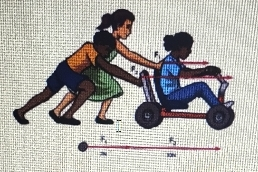
"\如题所述，两个力 $F_1$ 和 $F_2$ 作用在玩具滑板上。在给定的图中，很明显，$F_1$ 和 $F_2$ 两个力都沿同一方向作用在玩具滑板上。因此，作用在玩具上的合力 $F_{net}=F_1+F_2$
半透明物体也会投射阴影，但它不会像不透明物体投射的阴影那样暗。因为不透明物体完全阻挡光线，而半透明物体不会完全阻挡光线，允许一些光线穿过它。
已知：两个有理数是 $\frac{1}{4}$ 和 $\frac{1}{2}$。要求：我们必须找到这两个给定有理数之间的三个有理数。解：要解决这个问题，首先我们需要找到分母的最小公倍数并将它们转换为同类分数。分母 4 和 2 的最小公倍数是 4。要转换为同类分数，我们将 $\frac{1}{2}$ 的分子和分母都乘以 2。$\frac{1}{ 2} = \frac{1}{2}\times\frac{2}{2} = \frac{2}{4}$现在我们的数字是 $\frac{1}{4}$ 和 $\frac{2}{4}$。现在在分子 1 和 2 之间，没有整数。因此，我们必须再次将两个数字的分子和分母都乘以以查看是否有足够的数字。让 ... 阅读更多
要求：我们必须证明 \( \frac{12}{3+\sqrt{5}-2 \sqrt{2}}=\sqrt{10}+\sqrt{5}-\sqrt{2}+1 \)。解：对分母进行有理化，得到，$ \begin{array}{l}\frac{12}{3+\sqrt{5} -2\sqrt{2}} =\frac{12\left( 3+\sqrt{5} +2\sqrt{2}\right)}{\left( 3+\sqrt{5} -2\sqrt{2}\right)\left( 3+\sqrt{5} +2\sqrt{2}\right)}\\=\frac{36+12\sqrt{5} +24\sqrt{2}}{\left( 3+\sqrt{5}\right)^{2} -\left( 2\sqrt{2}\right)^{2}}\\=\frac{36+12\sqrt{5} +24\sqrt{2}}{9+5+6\sqrt{5} -8}\\=\frac{36+12\sqrt{5} +24\sqrt{2}}{6+6\sqrt{5}}\\=\frac{6+2\sqrt{5} +4\sqrt{2}}{1+\sqrt{5}}\\=\frac{6+2\sqrt{5} +4\sqrt{2}\left(\sqrt{5} -1\right)}{\left(\sqrt{5} +1\right)\left(\sqrt{5} -1\right)}\\=\frac{6\sqrt{5} -6+2\sqrt{5\times 5} -2\sqrt{5} +4\sqrt{2\times 5} -4\sqrt{2}}{5-1}\\=\frac{4\sqrt{5} -6+10+4\sqrt{10} -4\sqrt{2}}{4}\\=\frac{4\left(\sqrt{10} +\sqrt{5} -\sqrt{2} +1\right)}{4}\\=\sqrt{10} +\sqrt{5} -\sqrt{2} +1\end{array}$因此得证。 阅读更多
众所周知，对于静止在流体中的物体，浮力 = 浸没物体的重量。作用在浸没在流体中的物体上的力，$F=V\rho g$设物体的体积$=V$物体的密度$=\rho$ [已知]上层液体的密度$=\rho_{1}$ [已知]下层液体的密度$= \rho_{2}$ [已知]假设物体在上层液体的体积为 $v_1$，在下层液体的体积为 $v_2$。因此，$V=v_1+v_2$由于球体在界面处静止不动，如题所述，因此物体上的净浮力将等于物体的重量。设由于 ... 阅读更多
已知：\( 3^{3000}-3^{2999}-3^{2998}-3^{2997}=a \cdot 3^{2997} \)要求：我们必须找到 \( a \) 的值。解：$ \begin{array}{l}3^{3000} -3^{2999} -3^{2998} -3^{2997} =3^{2997}\left( 3^{3} -3^{2} -3^{1} -1\right)\\=3^{2997}( 27-9-3-1)\\=3^{2997}( 27-13)\\=14\ .\ 3^{2997}\end{array}$$=a \cdot 3^{2997}$比较两边，得到，$a=14$。$a$ 的值为 $14$。
已知：\( 25^{x-1}=5^{2 x-1}-100 \)要求：我们必须找到 $x$ 的值。解：$25^{x-1}=5^{2x-1}-100$$(5^2)^{x-1}=5^{2x-1}-100$$5^{2x-2}-5^{2x-1}=-100$$5^{2x-1}(5^{-1}-1)=-100$$5^{2x-1}(\frac{1}{5}-1)=-100$$5^{2x-1}(1-\frac{1}{5})=100$$5^{2x-1}(\frac{5-1}{5})=100$$5^{2x-1}(\frac{4}{5})=100$$5^{2x-1}(2^2)\times5^{-1}=(25\times4)$$5^{2x-2}(2^2)=(5^2\times2^2)$比较两边，得到，$2x-2=2$$2x=2+2$$2x=4$$x=2$因此，$x$ 的值为 $2$。