正确答案:(b) 煤油解释:由于液体没有固定的形状但有固定的体积,因此,煤油是正确选项。
正确答案:(c) 某些物质的粒子在不断运动解释:物质的粒子在三种状态(固态、液态和气态)下都处于不断运动的状态,因此,某些物质的粒子在不断运动的说法是不正确的。在固体中,粒子固定在它们的位置上,但它们会不断振动。
正确答案:(c) 溴比空气重解释:这里发生的现象是扩散,不受质量的影响。因此,溴比较重,与无色的空气混合。
正确答案:(c) 溴的粒子在运动,但空气的粒子没有运动解释:溴的粒子在运动,但空气的粒子没有运动的说法是不正确的,因为物质的粒子始终处于运动状态。看起来空气分子没有运动,因为空气是无色的。
正确答案:(b) 液体中的分子以规则的模式排列解释:在液体中,分子排列松散,而不是以规则的模式排列。因此,上述陈述不正确。
(a) 当两个广口瓶之间的玻璃板被移除时,红棕色气体将从广口瓶 A 扩散到无色广口瓶 B 中,反之亦然,因此红棕色将扩散到广口瓶 B 中。(b) 这里发生的现象是扩散。扩散是指气态原子和分子从相对高浓度区域转移到相对低浓度区域的过程。(c) 广口瓶 A 中可能是溴蒸气,因为溴呈红棕色。(d) 广口瓶 B 中可能是空气。(e) 高锰酸钾(有色固体)和水(无色液体)也表现出... 阅读更多
已知:球体的表面积为 $3844\ m^{2}$。要求:求球体的半径。解:球体的表面积为 $3844\ m^{2}$。设球体的半径为 $r$。$\Rightarrow$ 球体的表面积$=4\pi r^2=3844$$\Rightarrow r^2=\frac{3844}{4\pi}$$\Rightarrow r^2=\frac{3844}{4\times3.14}$$\Rightarrow r^2=305.80$$\Rightarrow r=\sqrt{305.80}$$\Rightarrow r=17.48\ m$因此,球体的半径为 $17.48\ m$。
已知:一个平行四边形,其边长为 $b$ 和 $h$,如图所示。要求:求出三角形的面积,然后求出平行四边形的面积。这个过程是否与我们已经知道的公式一致。解:两个三角形的面积$=2\times\frac{1}{2}\times b \times h$$=\frac{2}{2}\times b\times h$$=1\times b\times h$$=b\times h$平行四边形的面积$=$ 2 个三角形的面积$=b\times h$是的,它与我们之前知道的平行四边形面积公式 $b\times h$ 一致。
下面给出一个不完整的分布
| 变量 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-800 |
| 频率 | 12 | 30 | - | 65 | - | 25 | 18 |
已知:给出一个不完整的分布。中位数为 46,项目总数为 230。要求:我们必须使用中位数公式找到缺失的频率。解:设 $p_1$ 和 $p_2$ 为缺失的频率。中位数 $= 46$,$N = 230$$150 + p_1 + p_2 = 230$$p_1+p_2 = 230 - 150 = 80$$p_2 = 80-p_1$.....….(i)中位数 $= 46$,位于 40-50 类别$l = 40, f= 65, F = 42+p_1$ 和 $h = 50-40=10$中位数 $=l+(\frac{\frac{\mathrm{N}}{2}-\mathrm{F}}{f}) \times h$$46=40+\frac{\frac{230}{2}-(42+p_1)}{65}\times 10$$46-40=\frac{115-42-p_1}{13}\times2$$6(13)=(73-p_1)2$$39=73-p_1$$p_1=73-39=34$$p_2 = 80 - 34 = 46$ [从 (i) 得出]缺失的频率为 34 和 46。
**已知:**给定分布的平均值为 1.46。**求:**我们需要找到缺失的频数和中位数。**解:**平均值 $= 1.46$设 $p_1$ 和 $p_2$ 为如下所示的缺失频数。$86+p_1+p_2=200$$\Rightarrow p_1+p_2=200-86=114$$p_1=114-p_2$...............(i)我们知道,平均值 $=\frac{\sum f_i x_i}{\sum f_i}$因此,平均值 $=\frac{140+p_1+2 p_2}{200}$$\Rightarrow 1.46=\frac{140+p_1+2 p_2}{200}$$\Rightarrow 292=140+p_1+2 p_2$$\Rightarrow 292-140=114-p_2+2 p_2$ [由 (i) 式]$\Rightarrow 152-114= p_2$$\Rightarrow p_2=38$$\Rightarrow p_1=114-38=76$因此,$N = 86+76+38=200$$\frac{N}{2} = \frac{200}{2} = 100$累积频数刚好大于 $\frac{N}{2}=100$ 是 122(=46+76),对应于 122 的值为 1。这意味着,中位数 $=1$缺失的频数为 76 和 38,中位数为 1。 阅读更多

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
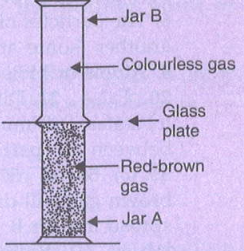 (a) 当两个广口瓶之间的玻璃板被移除时会发生什么?(b) 发生的现象叫什么?(c) 广口瓶 A 中可能存在的棕色气体是什么?(d) 广口瓶 B 中最有可能存在的无色气体是什么?(e) 说出一种可以表现出相同现象的有色固体和一种无色液体。
(a) 当两个广口瓶之间的玻璃板被移除时会发生什么?(b) 发生的现象叫什么?(c) 广口瓶 A 中可能存在的棕色气体是什么?(d) 广口瓶 B 中最有可能存在的无色气体是什么?(e) 说出一种可以表现出相同现象的有色固体和一种无色液体。 "\
"\