数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
(a) 碳原子可以形成大量的化合物是因为碳是四价的且原子半径小，因此可以形成稳定的共价键（链状结构）。(b) 燃气灶的进气孔需要经常调整，以便空气能够通过，从而实现完全燃烧。燃料不完全燃烧会导致烟炱的形成，从而使容器变黑。(c) 合成洗涤剂的使用会导致水污染，因为它们是不可生物降解的，因此不容易分解。
当铁制品在潮湿的空气（或水中）中放置相当长的时间后，它会被一种叫做铁锈的红棕色片状物质覆盖。这个过程被称为生锈。实验：在装有铁钉的试管A中，我们加入未煮沸的水，使铁钉的大约三分之二浸在水中，其余部分露出水面，暴露在潮湿的空气中。这样，第三个试管中的铁钉就同时置于空气和水中。在装有铁钉的试管B中，我们加入煮沸的蒸馏水。煮沸的水不含任何溶解的空气（或氧气）…… 阅读更多
(a) 硫酸亚铁晶体呈浅绿色，含有水分子 (FeSO4·7H2O)。加热时，硫酸亚铁晶体失去水分子，形成白色无水硫酸亚铁 (FeSO4)。强烈加热后，它变成棕色的氧化铁。(b) 强烈加热硫酸亚铁晶体后形成的产物是氧化铁、二氧化硫和三氧化硫。这是一种分解反应（热分解）。反应的化学方程式如下：$FeSO_4·7H_2O (s) \rightarrow FeSO_4 + 7H_2O$$2FeSO_4 (s) \rightarrow Fe_2O_3(s) + SO_2(g) + SO_3(g) $
证明：我们需要证明 \( \sqrt{\frac{1+\sin A}{1-\sin A }}=\sec A+\tan A \)。解：我们知道，$\frac{1}{\cos\ A}=\sec\ A$$\frac{\sin\ A}{\cos\ A}=\tan\ A$$sin^2\ A+cos^2\ A=1$左边$\sqrt{\frac{1+\sin A}{1-\sin A }}=(\sqrt{\frac{1+\sin A}{1-\sin A }})\times\sqrt{\frac{1+\sin A}{1+\sin A }}$ (分母有理化)$=\sqrt{\frac{(1+\sin A)^2}{1^2-\sin^2 A }}$$=\sqrt{\frac{(1+\sin A)^2}{\sin^2\ A+\cos^2\ A-\sin^2 A }}$$=\frac{1+\sin A}{\cos\ A}$$=\frac{1}{\cos\ A}+\frac{\sin\ A}{\cos\ A}$$=\sec\ A+\tan\ A$因此证明成立。
已知：\( \frac{3 \sqrt{2}}{3 \sqrt{2}-2 \sqrt{2}} \)解：我们需要找到有理化后的分母。解：我们知道，分母为 $a-\sqrt{b}$ 的分数的有理化因子是 $a+\sqrt{b}$。因此，$\frac{3 \sqrt{2}}{3 \sqrt{2}-2 \sqrt{2}}=\frac{3 \sqrt{2}}{3 \sqrt{2}-2 \sqrt{2}}\times\frac{3 \sqrt{2}+2 \sqrt{2}}{3 \sqrt{2}+2 \sqrt{2}}$$=\frac{3\sqrt2(5\sqrt2)}{(3\sqrt2)^2-(2\sqrt2)^2}$$=\frac{15\times2}{18-8}$$=\frac{30}{10}$$=3$有理化后的分母是10。
解：我们需要对给定表达式的分母进行有理化。解：我们知道，分母为 ${\sqrt{a}}$ 的分数的有理化因子是 ${\sqrt{a}}$。分母为 ${\sqrt{a}-\sqrt{b}}$ 的分数的有理化因子是 ${\sqrt{a}+\sqrt{b}}$。因此， (i) $\frac{1}{\sqrt{7}}=\frac{1}{\sqrt{7}}\times\frac{\sqrt{7}}{\sqrt{7}}$$=\frac{\sqrt{7}}{(\sqrt{7})^2}$$=\frac{\sqrt{7}}{7}$。(ii) $\frac{1}{\sqrt{7}-\sqrt{6}}=\frac{1}{\sqrt{7}-\sqrt{6}}\times\frac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}$$=\frac{\sqrt{7}+\sqrt{6}}{(\sqrt{7})^2-(\sqrt{6})^2}$$=\frac{\sqrt{7}+\sqrt{6}}{7-6}$$=\sqrt{7}+\sqrt{6}$。(iii) $\frac{1}{\sqrt{5}+\sqrt{2}}=\frac{1}{\sqrt{5}+\sqrt{2}}\times\frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}$$=\frac{\sqrt{5}-\sqrt{2}}{(\sqrt{5})^2-(\sqrt{2})^2}$$=\frac{\sqrt{5}-\sqrt{2}}{5-2}$$=\frac{\sqrt{5}-\sqrt{2}}{3}$(iv) $\frac{1}{\sqrt{7}-2}=\frac{1}{\sqrt{7}-2}\times\frac{\sqrt{7}+2}{\sqrt{7}+2}$$=\frac{\sqrt{7}+2}{(\sqrt{7})^2-(2)^2}$$=\frac{\sqrt{7}+2}{7-4}$$=\frac{\sqrt{7}+2}{3}$。阅读更多
解：我们需要将给定的数字分类为有理数或无理数。解： (i) $\sqrt{23}=4.795831523..........$\( \sqrt{23} \) 的十进制展开是非终止且非循环的。因此，\( \sqrt{23} \) 是一个无理数。(ii) $\sqrt{225}=15$\( \sqrt{225} \) 的十进制展开是终止的。因此，\( \sqrt{225} \) 是一个有理数。(iii) \( 0.3796 \)数字 $0.3796$ 是终止的。因此，它是有理数。(iv) \( 7.478478 \ldots \)数字 $7.478478$ 是非终止但循环的。因此，它是有理数。(v) \( 1.101001000100001 \ldots \)数字 $1.101001000100001…..$ 是非终止非循环的。因此，它是一个无理数。
已知：给定项为 $(x + 1)$。给定的多项式为：(i) \( x^{3}+x^{2}+x+1 \)(ii) \( x^{4}+x^{3}+x^{2}+x+1 \)解：我们需要检查给定的多项式是否具有 $(x + 1)$ 因子。解：根据因式定理，如果 $(x+1)$ 是给定多项式 $P(x)$ 的一个因子，那么在 $x= -1$ 时，$p(x)=0$。(i) $x^{3}+x^{2}+x+1$设 $p(x)= x^{3}+x^{2}+x+1$代入 $x= -1$$p(−1)=(−1)^3+(−1)^2+(−1)+1 =−1+1−1+1=0$因此，根据因式定理，$x+1$ 是 $x^{3}+x^{2}+x+1$ 的一个因子。(ii) $x^{4}+x^{3}+x^{2}+x+1$设 $p(x)=x^{4}+x^{3}+x^{2}+x+1$代入 $x= -1$$p(−1)=(−1)^4+(-1)^3+(−1)^2+(−1)+1 =1−1+1−1+1=1$因此，根据因式定理，$x+1$ 不是 $x^{4}+x^{3}+x^{2}+x+1$ 的一个因子。阅读更多
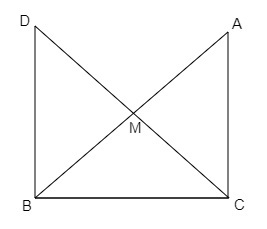
"\已知：在直角三角形ABC中，∠C为直角。M是斜边AB的中点。C与M连接并延长到点D，使得DM=CM。点D与点B连接。