数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究下列哪些是放热过程？（i）水与生石灰的反应（ii）酸的稀释（iii）水的蒸发（iv）樟脑（晶体）的升华
| (a) (i) 和 (ii) | (b) (ii) 和 (iii) |
| (c) (i) 和 (iv) | (d) (ii) 和 (iv) |
正确答案： (a) (i) 和 (ii) 解释：水与生石灰的反应和酸的稀释会释放热能。因此，这是一个放热反应。
取三个分别标记为 A、B 和 C 的烧杯，每个烧杯中各盛有 25 毫升水。在 A、B 和 C 烧杯中分别加入少量 NaOH、无水 CuSO4 和 NaCl。观察到 A 和 B 烧杯中溶液的温度升高，而 C 烧杯中溶液的温度下降。下列哪个陈述是正确的？(i) 在 A 和 B 烧杯中发生了放热过程。
(ii) 在 A 和 B 烧杯中发生了吸热过程。
(iii) 在 C 烧杯中发生了放热过程。
(iv) 在 C 烧杯中发生了吸热过程。
| (a) 仅 (i) | (b) 仅 (ii) |
| (c) (i) 和 (iv) | (d) (iv)
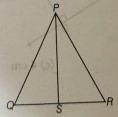
正确答案： (c) (i) 和 (iv) 解释：A 烧杯中发生的反应：$NaOH + H_2O → Na^+ + OH^− + H_2O + 热量$ B 烧杯中发生的反应：$CuSO_4(s) + 5H_2O(l) → CuSO_4.5H_2O(s) + 热量$ 因此，A 和 B 都是放热反应，导致温度升高。另一方面，C 烧杯中发生的是吸热反应，因为热量被吸收，导致温度下降。$NaCl + H_2O + 热量→Na^+ + Cl^− + H_2O$ 加法逆元：一个数的加法逆元是指当它与原数相加时结果为零的数。例如，求 -10 的加法逆元。设 x 为加法逆元。如果 x 是 -10 的加法逆元，则以下等式必须成立：$x + (-10) = 0$ 在两边都加上 10 $x + (-10) +10 = 10$ $x = 10$ 所以，10 是 -10 的加法逆元。乘法逆元：乘法逆元是指使现有数字等于一的数字。a 的乘法逆元是 $\frac{1}{a}$。例如，$\frac{-3}{6}$ 的乘法逆元是 $\frac{1}{\frac{-3}{6}}$ $= \frac{6}{-3} = \frac{-6}{3} = -2$。阅读更多 已知：$PR>PQ$ 且 PS 平分 $\angle QPR$。要做：我们必须证明 \( \angle PSR>\angle PSQ \)。解答：我们知道，较大边所对的角是较大角。这意味着，\( \angle PQR>\angle PRQ \)\( \angle QPS=\angle RPS \) (PS 平分 $\angle QPR$) 设 \( \angle QPS=\angle RPS=x \) 在三角形 PQS 中，$\angle PSR=\angle PQR+x$......(i) (外角性质) 在三角形 PSR 中，$\angle PSQ=\angle PRQ+x$......(ii) (外角性质)\( \angle PQR>\angle PRQ \) (已知) 在两边都加上 x，\( \angle PQR + x ... 阅读更多 已知：给定的方程组为：$2ax+3by=a+2b$ $3ax+2by=2a+b$ 要做：这里，我们必须用十字相乘法解给定的方程组。解答： 给定的方程组可以写成， $2ax+3by-(a+2b)=0$ $3ax+2by-(2a+b)=0$ 线性方程对（标准形式）$a_1x+b_1y+c_1=0$ 和 $a_2x+b_2y+c_2=0$ 的解由下式给出，$\frac{x}{b_1c_2-b_2c_1}=\frac{-y}{a_1c_2-a_2c_1}=\frac{1}{a_1b_2-a_2b_1}$ 将给定的方程与方程的标准形式进行比较，我们得到，$a_1=2a, b_1=3b, c_1=-(a+2b)$ 和 $a_2=3a, b_2=2b, c_2=-(2a+b)$ 因此，$\frac{x}{3b\times-(2a+b)-(2b)\times-(a+2b)}=\frac{-y}{2a\times-(2a+b)-3a\times-(a+2b)}=\frac{1}{2a\times(2b)-3a\times (3b)}$ $\frac{x}{-6ab-3b^2+2ab+4b^2}=\frac{-y}{-4a^2-2ab+3a^2+6ab}=\frac{1}{4ab-9ab}$ $\frac{x}{-4ab+b^2}=\frac{-y}{-a^2+4ab}=\frac{1}{-5ab}$ $\frac{x}{-4ab+b^2}=\frac{1}{-5ab}$ 和 $\frac{-y}{-a^2+4ab}=\frac{1}{-5ab}$ $x=\frac{(-4ab+b^2)\times1}{-5ab}$ 和 $-y=\frac{(-a^2+4ab)\times1}{-5ab}$ $x=\frac{-b(4a-b)}{-5ab}$ 和 $-y=\frac{-a(a-4b}{-5ab}$ $x=\frac{4a-b}{5a}$ 和 $-y=\frac{a-4b}{5b}$ $x=\frac{4a-b}{5a}$ 和 $y=\frac{4b-a}{5b}$ 给定方程组的解是 $x=\frac{4a-b}{5a}$ 和 $y=\frac{4b-a}{5b}$。阅读更多 已知：给定的方程组为：$5ax+6by=28$ $3ax+4by=18$ 要做：这里，我们必须用十字相乘法解给定的方程组。解答： 给定的方程组可以写成， $5ax+6by-28=0$ $3ax+4by-18=0$ 线性方程对（标准形式）$a_1x+b_1y+c_1=0$ 和 $a_2x+b_2y+c_2=0$ 的解由下式给出，$\frac{x}{b_1c_2-b_2c_1}=\frac{-y}{a_1c_2-a_2c_1}=\frac{1}{a_1b_2-a_2b_1}$ 将给定的方程与方程的标准形式进行比较，我们得到，$a_1=5a, b_1=6b, c_1=-28$ 和 $a_2=3a, b_2=4b, c_2=-18$ 因此，$\frac{x}{6b\times(-18)-(4b)\times(-28)}=\frac{-y}{5a\times(-18)-3a\times(-28)}=\frac{1}{5a\times(4b)-3a\times (6b)}$ $\frac{x}{-108b+112b}=\frac{-y}{-90a+84a}=\frac{1}{20ab-18ab}$ $\frac{x}{4b}=\frac{-y}{-6a}=\frac{1}{2ab}$ $x=\frac{4b\times1}{2ab}$ 和 $-y=\frac{(-6a)\times1}{2ab}$ $x=\frac{2}{a}$ 和 $-y=\frac{-3}{b}$ $x=\frac{2}{a}$ 和 $y=\frac{3}{b}$ 给定方程组的解是 $x=\frac{2}{a}$ 和 $y=\frac{3}{b}$。阅读更多 已知：给定的方程组为：$(a+2b)x+(2a-b)y=2$ $(a-2b)x+(2a+b)y=3$ 要做：这里，我们必须用十字相乘法解给定的方程组。解答： 给定的方程组可以写成， $(a+2b)x+(2a-b)y-2=0$ $(a-2b)x+(2a+b)y-3=0$ 线性方程对（标准形式）$a_1x+b_1y+c_1=0$ 和 $a_2x+b_2y+c_2=0$ 的解由下式给出，$\frac{x}{b_1c_2-b_2c_1}=\frac{-y}{a_1c_2-a_2c_1}=\frac{1}{a_1b_2-a_2b_1}$ 将给定的方程与方程的标准形式进行比较，我们得到，$a_1=(a+2b), b_1=(2a-b), c_1=-2$ 和 $a_2=(a-2b), b_2=(2a+b), c_2=-3$ 因此，$\frac{x}{(2a-b)\times(-3)-(2a+b)\times(-2)}=\frac{-y}{(a+2b)\times(-3)-(a-2b)\times(-2)}=\frac{1}{(a+2b)\times(2a+b)-(a-2b)\times (2a-b)}$ $\frac{x}{-6a+3b+4a+2b}=\frac{-y}{-3a-6b+2a-4b}=\frac{1}{2a^2+ab+4ab+2b^2-2a^2+ab+4ab-2b^2}$ $\frac{x}{-2a+5b}=\frac{-y}{-a-10b}=\frac{1}{10ab}$ $x=\frac{(5b-2a)\times1}{10ab}$ 和 $-y=\frac{(-a-10b)\times1}{10ab}$ $x=\frac{5b-2a}{10ab}$ 和 $-y=\frac{-a-10b}{10ab}$ $x=\frac{5b-2a}{10ab}$ 和 $y=\frac{a+10b}{10ab}$ 给定方程组的解是 $x=\frac{5b-2a}{10ab}$ 和 $y=\frac{a+10b}{10ab}$。 阅读更多 已知：给定的方程组为：$x(a-b+\frac{ab}{a-b})=y(a+b-\frac{ab}{a+b})$ $x+y=2a^2$ 要求：这里，我们要求解给定的方程组，方法是十字相乘法。解答：给定的方程组可以写成： $x(a-b+\frac{ab}{a-b})=y(a+b-\frac{ab}{a+b})$ $x[\frac{(a-b)^2+ab}{a-b}]-y[\frac{(a+b)^2-ab}{a+b}]=0$ $x(\frac{a^2+b^2-2ab+ab}{a-b})-y(\frac{a^2+b^2+2ab-ab}{a+b})=0$ $x(\frac{a^2+b^2-ab}{a-b})-y(\frac{a^2+b^2+ab}{a+b})=0$.....(i) $x+y-2a^2=0$....(ii)线性方程组$a_1x+b_1y+c_1=0$和$a_2x+b_2y+c_2=0$的解由下式给出： $\frac{x}{b_1c_2-b_2c_1}=\frac{-y}{a_1c_2-a_2c_1}=\frac{1}{a_1b_2-a_2b_1}$将给定的方程与标准形式的方程进行比较，得到： $a_1=(\frac{a^2+b^2-ab}{a-b}), b_1=-(\frac{a^2+b^2+ab}{a+b}), c_1=0$ 和 $a_2=1, b_2=1, c_2=-2a^2$因此， $\frac{x}{(-2 a^{2})[-(\frac{a^{2}+b^{2}+a b}{a+b})]-0 \times 1}=\frac{-y}{(-2 a^{2})(\frac{a^{2}+b^{2}-a b}{a-b})-0 \times 1}=\frac{1}{\frac{a^{2}+b^{2}-a b}{a-b}-[-\frac{(a^{2}+b^{2}+a b)}{a+b}]}$ $\frac{x}{2 a^{2}\left(\frac{a^{2}+b^{2}+a b}{a+b}\right)}=\frac{y}{\left(2 a^{2}\right)\left(\frac{a^{2}+b^{2}-a b}{a-b}\right)}=\frac{1}{\frac{a^{2}+b^{2}-a b}{a-b}+\frac{a^{2}+b^{2}+a b}{a+b}}$ $\frac{x}{2 a^{2}\left(\frac{a^{2}+b^{2}+a b}{a+b}\right)}=\frac{y}{2 a^{2}\left(\frac{a^{2}+b^{2}-a b}{a-b}\right)}=\frac{(a-b)(a+b)}{(a+b)\left(a^{2}+b^{2}-a b\right)+(a-b)\left(a^{2}+b^{2}+a b\right)}$ $\frac{x}{2 a^{2}\left(\frac{a^{2}+b^{2}+a b}{a+b}\right)}=\frac{y}{2 a^{2}\left(\frac{a^{2}+b^{2}-a b}{a-b}\right)}=\frac{(a-b)(a+b)}{a^{3}+b^{3}+a^{3}-b^{3}}$ $\frac{x}{2 a^{2}\left(\frac{a^{2}+b^{2}+a b}{a+b}\right)}=\frac{y}{2 a^{2}\left(\frac{a^{2}+b^{2}-a b}{a-b}\right)}=\frac{(a-b)(a+b)}{2a^3/(a-b)(a+b)}$ …… 阅读更多 已知：给定的方程组为：$bx+cy=a+b$ $ax(\frac{1}{a-b}-\frac{1}{a+b})+cy(\frac{1}{b-a}-\frac{1}{b+a})=\frac{2a}{a+b}$ 要求：这里，我们要求解给定的方程组，方法是十字相乘法。解答：给定的方程组可以写成： $bx+cy-(a+b)=0$....(i) $ax(\frac{1}{a-b}-\frac{1}{a+b})+cy(\frac{1}{b-a}-\frac{1}{b+a})=\frac{2a}{a+b}$ $ax(\frac{a+b-(a-b)}{(a-b)(a+b)})+cy(\frac{b+a-(b-a)}{(b-a)(b+a)})-\frac{2a}{a+b}=0$ $\frac{1}{a+b}[ax(\frac{a+b-a+b}{a-b})+cy(\frac{b+a-b+a}{b-a})-2a]=0$ $ax(\frac{2b}{a-b})-cy(\frac{2a}{a-b})-\frac{2a(a-b)}{a-b}=0$ $\frac{ax(2b)-cy(2a)-2a(a-b)}{a-b}=0$ $2abx-2acy-2a(a-b)=0$...(ii)线性方程组$a_1x+b_1y+c_1=0$和$a_2x+b_2y+c_2=0$的解由下式给出： $\frac{x}{b_1c_2-b_2c_1}=\frac{-y}{a_1c_2-a_2c_1}=\frac{1}{a_1b_2-a_2b_1}$将给定的方程与标准形式的方程进行比较，得到： $a_1=b, b_1=c, c_1=-(a+b)$ 和 $a_2=2ab, b_2=-2ac, c_2=-2a(a-b)$因此， $\frac{x}{-2 a c(a-b)-[-(a+b)][-2 a c]}=\frac{-y}{-2 a b(a-b)-[-(a+b)][2 a b]}=\frac{1}{-2 a b c-2 a b c}$ $\frac{x}{-2 a^{2} c+2 a b c-\left[2 a^{2} c+2 a b c\right]}=\frac{-y}{-2 a^{2} b+2 a b^{2}+\left[2 a^{2} b+2 a b^{2}\right]}=\frac{1}{-4 a b ... 阅读更多 已知：给定的方程组为：$(a-b)x+(a+b)y=2a^2-2b^2$ $(a+b)(x+y)=4ab$ 要求：这里，我们要求解给定的方程组，方法是十字相乘法。解答：给定的方程组可以写成： $(a-b)x+(a+b)y-2(a^2-b^2)=0$....(i) $(a+b)(x+y)=4ab$ $(a+b)x+(a+b)y-4ab=0$......(ii)线性方程组$a_1x+b_1y+c_1=0$和$a_2x+b_2y+c_2=0$的解由下式给出： $\frac{x}{b_1c_2-b_2c_1}=\frac{-y}{a_1c_2-a_2c_1}=\frac{1}{a_1b_2-a_2b_1}$将给定的方程与标准形式的方程进行比较，得到： $a_1=(a-b), b_1=(a+b), c_1=-2(a^2-b^2)$ 和 $a_2=(a+b), b_2=(a+b), c_2=-4ab$因此， $ \begin{array}{l}\frac{x}{( a+b)( -4ab) -( a+b) \times -2\left( a^{2} -b^{2}\right)} =\frac{-y}{( a-b)( -4ab) -( a+b) \times -2\left( a^{2} -b^{2}\right)} =\frac{1}{( a-b)( a+b) -( a+b)( a+b)}\\\\\frac{x}{2( a+b)\left[ -2ab+a^{2} -b^{2}\right]} =\frac{-y}{( a-b)( -4ab) +2( a+b)( a+b)( a-b)} =\frac{1}{( ... 阅读更多 广告
|
"\