已知:在三角形 PQR 中,PS=2 厘米,QR=4 厘米。在三角形 LMN 中,LO=2 厘米,MN=3 厘米。求解:我们需要求出给定三角形的面积。解:我们知道,高为 h,底为 b 的三角形的面积为 1/2bh。(i) 在三角形 PQR 中,高=PS=2 厘米,底=QR=4 厘米。三角形 PQR 的面积=1/2×2×4 平方厘米=4 平方厘米。(ii) 在三角形 LMN 中,高=LO=2 厘米,底=MN=3 厘米。三角形 LMN 的面积=1/2×2×3 平方厘米=3 平方厘米。
已知:圆的周长为:(a) 22 厘米(b) 17.6 厘米(c) 30.8 厘米求解:我们需要求出圆的半径。解:(a) 设圆的半径为 r。这意味着,2πr=22 厘米2×22/7×r=22r=7×22/44r=7/2 厘米圆的半径为 3.5 厘米。(b) 设圆的半径为 r。这意味着,2πr=17.6 厘米2×22/7×r=17.6r=7×17.6/44r=7×0.4 厘米r=2.8 厘米圆的半径为 2.8 厘米。(c) 设圆的半径为 r。这意味着,2πr=30.8 厘米2×22/7×r=30.8r=7×30.8/44r=7×0.7 厘米r=4.9 厘米圆的半径为 4.9 厘米。阅读更多
已知:(3/5 × -15/21) + (-9/14 ÷ 45/28) - (2/3 × 30/12)求解:我们需要化简给定的表达式。解:(3/5 × -15/21) + (-9/14 ÷ 45/28) - (2/3 × 30/12)=1×-3/1×7 + -9/14 × 28/45 - 1×10/1×6=-3/7 + -1×2/1×5 - 10/6=-3/7 - 2/5 - 5/3=-(3/7 + 2/5 + 5/3)=-(3×15 + 2×21 + 5×35)/105=-(45 + 42 + 175)/105=-262/105因此,(3/5 × -15/21) + (-9/14 ÷ 45/28) - (2/3 × 30/12)=-262/105。阅读更多
已知:一个数的 3/2 是 42。求解:我们需要求出这个数。解:假设所需的数字为 x。这意味着,3/2×x=42x=2×42/3x=2×14x=28所需的数字是 28。
已知:0.04 ÷ 100求解:我们需要计算给定的表达式。解:0.04 ÷ 100=0.04/100=4×10^-2/10^2=4×10^-2-2=4×10^-4=0.0004因此,0.04 ÷ 100=0.0004。
(i) 18Ar 和 2He 是非常稳定的元素,因为它们是惰性气体。(ii) 20Ca 和 4Be 位于元素周期表第 2 族,因为每个元素的价电子数为 2。(iii) 8O 和 16S 位于元素周期表第 16 族,因为每个元素的价电子数为 6。
(a) Mg 的原子半径大于 Cl,因为在元素周期表的同一周期中,从左到右原子半径逐渐减小。(b) K 的原子半径大于 Na,因为在元素周期表的同一族中,从上到下原子半径逐渐增大。
三个元素 A、B 和 C 的原子序数如下:元素 原子序数
| A 5 | 5 |
| B 15 | 7 |
| C 10 | 10 |
(i) 哪个元素属于第 18 族?
(ii) 哪个元素属于第 15 族?
(iii) 哪个元素属于第 13 族?
(iv) 这些元素属于哪个周期?"
(i) 元素 C 属于第 18 族,因为元素 C(10)的电子构型为 2,8(ii) 元素 B 属于第 15 族,因为元素 B(15)的电子构型为 2,8,5(iii) 元素 A 属于第 13 族,因为元素 A(5)的电子构型为 2,3(iv) 元素 A、B 和 C 都属于第二周期,因为所有三个元素的最外层电子层相同,即 L 层。
(a) 元素 X 有 2 个价电子,因为它属于第二族。(b) 由于第二族元素的价电子数和化合价均为 2,因此元素 X 的化合价为 2。(c) 第二族位于元素周期表左侧,包含金属元素。因此,元素 X 是一种金属。(d) 元素的名称是镁(Mg),因为 X 属于第二族和第三周期。
已知,游泳池长度 = 90 米时间 = 1 分钟 = 60 秒(将分钟转换为秒)根据题意,乌莎从 A 游到 B,然后沿着同一条直线路径返回,从 B 游到 A。因此,乌莎在 1 分钟内行驶的总距离 = 90 + 90 = 180 米,乌莎在 1 分钟内的位移 = 0 米(因为她回到了初始位置)现在,我们知道-平均速度=总行程/总时间=180/60=3 米/秒平均速度=位移/时间=0/60=0 米/秒因此,乌莎的平均速度为 3 米/秒,她的平均速度为 0 米/秒。

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP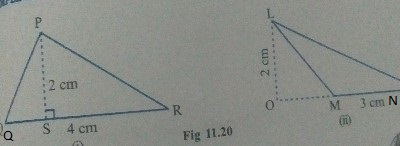 "\
"\