数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：一条长 8 米 54 厘米的丝带被剪成 7 段等长的丝带。求：我们必须找到每段丝带的长度。解：我们知道，$1\ m=100\ cm$丝带的总长度 $= 8\ m\ 54\ cm$。$=(8\times100+54)\ cm$$=(800+54)\ cm$$=854\ cm$要剪成的段数 $= 7$。每段丝带的长度 $= \frac{丝带的总长度}{段数}$$=\frac{854}{7}$$=122\ cm$$=\frac{122}{100}\ m$$=1.22\ m$每段丝带的长度为 $1.22\ m$。
已知：\( \frac{11}{2} x^{2} y-\frac{9}{4} x y^{2}+\frac{1}{4} x y-\frac{1}{14} y^{2} x+\frac{1}{15} y x^{2}+\frac{1}{2} x y \)。要做的：我们必须简化给定的表达式。解：我们知道，在表达式中可以加减同类项。因此， $\frac{11}{2} x^{2} y-\frac{9}{4} x y^{2}+\frac{1}{4} x y-\frac{1}{14} y^{2} x+\frac{1}{15} y x^{2}+\frac{1}{2} x y=(\frac{11}{2}+\frac{1}{15})x^2y-(\frac{9}{4}+\frac{1}{14})xy^2+(\frac{1}{4}+\frac{1}{2})xy$$=\left(\frac{11\times 15+1\times 2}{30}\right) x^{2} y-\left(\frac{9\times 7+1\times 2}{28}\right) xy^{2} +\left(\frac{1+1\times 2}{4}\right) xy$$=\left(\frac{165+2}{30}\right) x^{2} y-\left(\frac{63+2}{28}\right) xy^{2} +\left(\frac{1+2}{4}\right) xy$$=\frac{167}{30} x^{2} y-\frac{65}{28} xy^{2} +\frac{3}{4} xy$.阅读更多
正确答案是选项 b。森林无法生长和再生。除了选项 (b.)，所有其他选项都是正确的，a. 森林有助于防止水土流失 - 因为它们通过根部固定土壤。c. 森林可以影响气候 - 它们通过释放氧气和二氧化碳来影响气候，蒸腾作用在降雨中也起着重要作用。d. 森林可以改善空气质量 - 通过释放大量氧气。b. 森林无法生长和再生 - 因为树木是有生命的，它们可以生长并再生。因此，它是错误的。
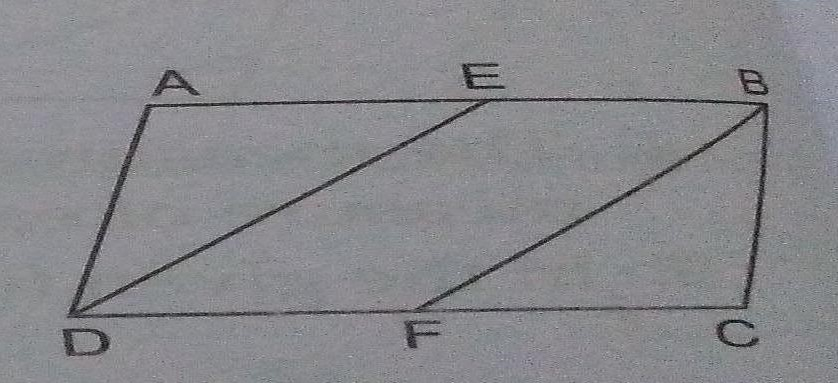
"\已知：ABCD 是一个平行四边形。\( B E=\frac{1}{2} A B \) 和 \( D F=\frac{1}{2} D C \)。要做的：我们必须证明 BEDF 是一个平行四边形。解：$AE=BE=\frac{1}{2}AB$$CF=DF=\frac{1}{2}CD$因此，$BE=DF$ (因为 $AB=CD$，平行四边形的对边相等)$BE\parallel DF$ 这意味着，BEDF 是一个平行四边形。证毕。
已知：$\frac{sin\theta}{cot\theta+cosec\theta}=2+\frac{sin\theta}{cot\theta-cosec\theta}$。要做的：证明 $L.H.S.=R.H.S.$解：$L.H.S. =\frac{sin\theta}{cot\theta+cosec\theta}$$= \frac{sin\theta}{\frac{cos\theta}{sin\theta}+\frac{1}{sin\theta}}$$= \frac{sin\theta}{\frac{cos\theta+1}{sin\theta}}$$= \frac{sin^{2}\theta}{(1+cos\theta)}$$= \frac{(1-cos^{2}\theta)}{(1+cos\theta)}$ $\because sin^{2}\theta = 1 - cos^{2}\theta$$= \frac{[( 1+cos\theta)( 1-cos\theta)]}{( 1+cos\theta)}$ $\because a^{2}-b^{2} = ( a+b)( a-b)$$= 1 - cos\theta ......( 1)$$R.H.S. = 2+ \frac{sin\theta}{(cot\theta-cosec\theta)}$$= 2+\frac{sin\theta}{\frac{cos\theta}{sin\theta}-\frac{1}{sin\theta}}$$= 2+\frac{sin\theta}{\frac{cos\theta-1}{sin\theta}}$$= 2+ \frac{[ sin^{2}\theta}{(cos\theta-1)]}$$= 2 - \frac{( sin^{2}\theta)}{( 1-cos\theta)}$$= 2- \frac{[ ( 1-cos^{2}\theta)}{( 1-cos\theta)]}$$= 2-\frac{[( 1+cos\theta)( 1-cos\theta)}{( 1-cos\theta)]}$$= 2 - ( 1+cos\theta)$$= 2-1-cos\theta$$= 1-cos\theta ......(2)$从 $( 1)$ & $( 2)$ ，我们得出结论，$( 1) = ( 2)$$L.H.S. = R.H.S.$阅读更多
已知：$\vartriangle ABC\sim\vartriangle RPQ,\ AB=3\ cm,\ BC=5\ cm,\ AC=6\ cm,\ RP=6\ cm\ and\ PQ=10\ cm$。要做的：求 $QR$。解： $\because\ \vartriangle ABC\sim\vartriangle PQR$如果两个三角形相似，则其对应边成比例。$\frac{RP}{AB}=\frac{PQ}{BC}=\frac{QR}{AC}$$\Rightarrow \frac{6}{3}=\frac{10}{5}=\frac{QR}{6}$$\Rightarrow \frac{QR}{6}=\frac{6}{3}$$\Rightarrow QR=\frac{6\times6}{3}$$\Rightarrow QR=12$因此 $QR=12\ cm$。
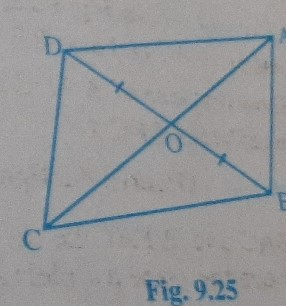
"\已知：在四边形 ABCD 中，对角线 \( A C \) 和 \( B D \) 相交于 \( O \)，使得 \( O B=O D \)。$AB = CD$。要做的：我们必须证明 $ar (DOC) = ar (AOB)$解：画 $DP \perp AC$ 和 $BQ \perp AC$。在 $\vartriangle DOP$ 和 $\vartriangle BOQ$ 中，$\angle DPO = \angle BQO=90^o$$\angle DOP = \angle BOQ$ (对顶角) $OD = OB$ (已知)$\vartriangle DOP \cong \vartriangle BOQ$ (根据 AAS 全等)因此，$DP = BQ$----(i) (全等三角形对应边相等)$ar(DOP) = ar(BOQ)$----(ii) (因为全等三角形的面积相等)在 $\vartriangle CDP$ 和 $\vartriangle ABQ$ 中，$\angle CPD = \angle AQB=90^o$$CD = AB$ ... 阅读更多
平行四边形：如果一个四边形有一对平行的对边，则称为平行四边形。平行四边形的性质如下：对边全等。对角相等。邻角互补。如果任何一个角是直角，则所有其他角也将是直角。两条对角线互相平分。每条对角线将平行四边形分成两个全等三角形。 $AB=CD$ 和 $AD=BC$$\angle A=\angle C$ 和 $\angle B=\angle D$$\angle A+\angle B=180^o$，$\angle A+\angle D=180^o$，$\angle B+\angle C=180^o$ 和 $\angle C+\angle D=180^o$。 阅读更多
已知：绳长 = 20 米。绳子与地面水平所成的角为 30°。