已知:给定数字为 18。任务:我们将 18 表示为两个素数之和的所有可能方式。解:素数:只有两个因数(1 和自身)的数。 $5 + 13 = 18,13 + 5 = 18$ $7 + 11 = 18,11 + 7 = 18$ 5、7、11、13 是素数。这些是将 18 表示为两个素数之和的可能方式。
已知:给定数字为 67。任务:我们必须列出至少三种不同的方法,将 67 表示为三个不同素数之和。解:素数:只有两个因数(1 和自身)的数。$3 + 5 + 59 = 67$ $3 + 11 + 53 = 67$ $7 + 13 + 47 = 67$ $11 + 13 + 43 = 67$ $7 + 19 + 41 = 67$ 这些是将 67 表示为三个不同素数之和的一些可能方式。
已知:5 打鸡蛋的成本价 = 每打 36 卢比,5 打鸡蛋中 5% 的鸡蛋坏了,剩余鸡蛋的售价 = 每打 48 卢比。求解:我们必须找到该人的总利润。解:1 打鸡蛋的成本价 = 36 卢比,5 打鸡蛋的成本价 = 36 × 5 卢比,5 打鸡蛋的成本价 = 180 卢比。现在,1 打鸡蛋中的鸡蛋数量 = 12,5 打鸡蛋中的鸡蛋数量 = 12 × 5,5 打鸡蛋中的鸡蛋数量 = 60。在 60 个鸡蛋中,5% 的鸡蛋坏了:60 个鸡蛋的 5% = 60\ ... 阅读更多
已知:$AB = QR,BC = RP,CA = PQ$。任务:我们必须找到正确顺序的三角形全等关系。解:已知,$AB = QR,BC = RP,CA = PQ$。两个三角形的对应边相等,因此它们全等。从上图中,我们可以匹配对应边。$\displaystyle 因此\ \triangle CBA\ \cong \ \triangle PRQ$。因此,选项 B 正确。
已知:$0.5(x-5)-0.2(9 x-4)=0.8$ 任务:系统地求解 解:$0.5(x-5)-0.2(9 x-4)=0.8$ 将两边乘以 10 $0.5(x-5) \cdot 10-0.2(9 x-4) \cdot 10=0.8 \cdot 10$ 简化 $5(x-5)-2(9 x-4)=8$ 展开 $5(x-5)-2(9 x-4):\quad-13 x-17$ $-13 x-17=8$ 在两边加上 17 $-13 x-17+17=8+17$ 简化 $-13 x=25$ 将两边除以 -13 $\frac{-13 x}{-13}=\frac{25}{-13}$ 简化 $x=-\frac{25}{13}$
已知:∠A = 120°,∠DBC = 2 ∠ABD,∠DCB = 2 ∠ACD。任务:我们必须找到∠BDC 的度数。解:设∠ABC = 3x,∠ACB = 3y这意味着∠ABD = x,∠CBD = 2x,∠ACD = y,∠DCB = 2y。我们知道,三角形内角和为 180°。因此,在三角形 ABC 中,$∠BAC + ∠ACB + ∠CBA = 180°$ $120° + ∠ACB + ∠CBA = 180°$ $∠ACB + ∠CBA = 180°-120°$ $3x + 3y = 60°$ $3(x+y) = 60°$ $x+y = \frac{60°}{3}$ $x+y=20°$ 设其为方程 (1)。在三角形 BDC 中,$∠BDC + ∠CBD + ∠DBC = 180°$ $∠BDC + 2x + 2y = 180°$ $∠BDC + 2(x+y) = 180°$ (根据方程 1) $∠BDC + 2(20°) = 180°$ $∠BDC + 40° = 180°$ $∠BDC = 180°-40°$ $∠BDC = 140°$ ∠BDC 的度数为 140°。
已知:三角形的角度之比为 4:3:14 求解:三角形的类型 解:三角形的角度之比为 4:3:14 设角度为 $4x, 3x, 14x$ 我们知道三角形的内角和为 $180^{\circ}$ 所以,$4x+3x+14x = 180^{\circ}$ $21x = 180^{\circ}$ $x= \frac{180^{\circ}}{21}$ $x= \frac{60^{\circ}}{7}$ 所以,角度为 $4\times\frac{60^{\circ}}{7}, 3\times\frac{60^{\circ}}{7},14\times\frac{60^{\circ}}{7}$ 它们是 $\frac{240^{\circ}}{7},\frac{180^{\circ}}{7},120^{\circ}$ 一个角度是 $120^{\circ}$,这是一个钝角(大于 90)所以,给定的三角形是钝角三角形。答案是 b
是的,即使另一个物体放在它们之间,两个物体之间也会存在万有引力。任何两个物体之间的万有引力只取决于两个因素:物体的质量和它们之间的距离。
互锁的意思是“两个物体完美地契合在一起,从而结合并一起移动”。当两个粗糙的表面相互接触时,如果每个表面的不规则性匹配,它们就会发生互锁。这会导致摩擦力。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
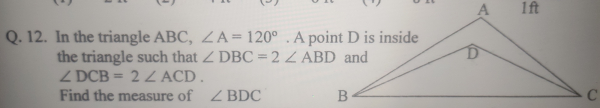 "\
"\