已知:直角三角形 求解:$x$ 解答:根据勾股定理公式: 斜边² = 高² + 底² (x+2)² = 5² + (x-3)² $(x+2)^{2}=5^{2}+(x-3)^{2}$$5^{2}=25$$(x+2)^{2}=25+(x-3)^{2}$展开 $(x+2)^{2}: x^{2}+4 x+4$展开 $25+(x-3)^{2}: \quad x^{2}-6 x+34$$x^{2}+4 x+4=x^{2}-6 x+34$两边减去 4$x^{2}+4 x+4-4=x^{2}-6 x+34-4$化简$x^{2}+4 x=x^{2}-6 x+30$两边减去 $x^{2}-6 x$ $x^{2}+4 x-\left(x^{2}-6 x\right)=x^{2}-6 x+30-\left(x^{2}-6 x\right)$化简$10 x=30$两边除以 10$\frac{10 x}{10}=\frac{30}{10}$化简$x=3$
需要证明:正方形的对角线相等且互相垂直平分。解答: 设 $ABCD$ 是一个正方形,其对角线 $AC$ 和 $BD$ 相交于点 $O$。在 $\triangle ABC$ 和 $\triangle BAD$ 中, $AB=AB$ (公共边)$BC=AD$ (正方形的四条边都相等)$\angle ABC= \angle BAD=90^o$因此,根据 SAS 全等,我们得到, $\triangle ABC \cong \triangle BAD$所以, $AC=BD$ (全等三角形对应边相等)对角线相等。在 $\triangle AOB$ 和 $\triangle COD$ 中, $\angle BAO = \angle DCO$ (内错角相等)$\angle AOB = ... 阅读更多
解答:假分数是指分子大于分母的分数。例如:$\frac{6}{5}$,$\frac{11}{3}$,$\frac{15}{9}$,等等都是假分数。带分数是指包含整数部分和真分数部分的分数。例如:$1\frac{1}{2}, 3 \frac{1}{3}, 10 \frac{1}{4}$,等等都是带分数。假分数可以转换为带分数通过将分子除以分母,并将商写成带分数的整数部分,余数/分母作为带分数的小数部分。例如:$\frac{9}{4} = 2 \frac{1}{4}; \frac{11}{5} = 2 \frac{1}{5}$,等等 ... 阅读更多
已知:$\frac{9x-7}{3x+5}=\frac{3x-4}{x+6}$ 求解:$x$ 的值 解答:交叉相乘, $ (9 x - 7) ( x + 6) = (3 x - 4) (3 x + 5 )$ =$9 x^{2} - 7 x + 54 x - 42 = 9 x^{2} - 12 x + 15 x - 20$ =$9 x^{2} - 7 x + 54 x - 42 - ( 9 x^{2} - 12 x + 15 x - 20)$ = 0 =$9 x^{2} - 7 x + 54 x - 42 - 9 x^{2} + 12 x - 15 x + 20 = 0$ [因为,$9 x ^{2} -9 x^{2} = 0$] =$- 7 x + 54 x + 12 x - 15 x - 42 + 20 = 0$ =$47 x - 3 x - 22 = 0$ =$44 x - 22 = 0$ =$44 x = 22$ =>$ x = \frac{22 }{44}$ 因此,$x = \frac{1}{2}$
已知:数字是 10.7 求解:数字的整数部分和小数部分 解答:小数 10.7 的整数部分是 10 小数 10.7 的小数部分是 0.7因此答案是 0.7
已知:三角形的周长 = 60 厘米。它的两条边分别长 15 厘米和 20 厘米。求解:三角形的第三条边解答:设三条边分别为 a、b、c。 a = 15 厘米 b = 20 厘米 c = ? 周长 = 所有边的和 $60 = a + b + c$ $60 = 15 + 20 + c$ $60 = 35 + c$ $60 - 35 = c$ $25 = c$ $c = 25$ 所以,三角形的第三条边是 25 厘米。
我们可以通过简单的触碰来区分的织物是:A. 雨衣和棉衬衫D. 毛衣和泳衣。
规则反射的优点 (i) 由于规则反射,我们可以在平面镜中看到自己的像 (ii) 潜望镜中成像是由于规则反射。规则反射的缺点:由于反射,物体变得有光泽,我们看不到物体本身,而是看到自己的像,因为它起到了镜子作用。为了看到物体,它必须不规则地反射光线。不规则反射的优点 (i) 任何不透明物体由于不规则反射而可见 (ii) 当一部电影 ... 阅读更多
已知:$y$ 的值为 1 求解:$2y^3 + 3y^2 + y - 3$ 的值 解答:$2y^3 + 3y^2 + y - 3$ 代入 $y$ = 1,$2(1)^3 +3(1)^2+ 1 - 3$ $2 (1) + 3 (1) - 2 = 2 + 3 - 2 = 5 - 2 = 3$ 当 y=1 时,$2y^3 + 3y^2 + y - 3$ 的值为 3。

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP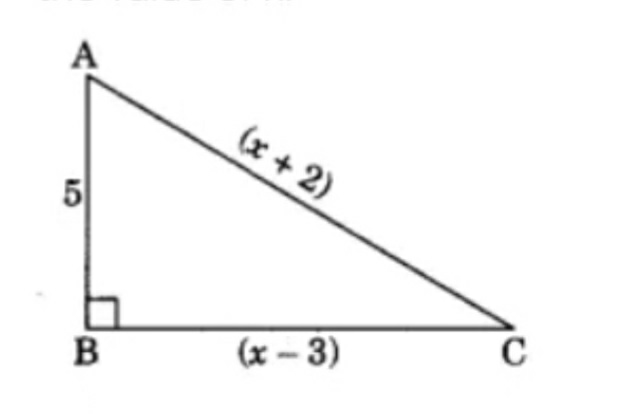 "\
"\