已知:在三角形 PQR 中,∠QRS = 125°;∠QPR = 65° 求解:我们需要求解∠PRQ 和∠PQR。 解答:∠PRQ 和∠QRS 构成一个线性对,因为它们是内角和外角 R ∠PRQ + ∠QRS = 180° ∠PRQ + 125° = 180°;所以 ∠PRQ = 180° - 125° = 55° 根据三角形 PQR 的内角和性质。 ∠PRQ + ∠PQR + ∠QPR = 180°;55° + ∠PQR + 65° = 180°;∠PQR = 180° - 120° = 60° 所以 ∠PRQ = 55° 且 ∠PQR = 60°
已知:3x = 639 求解:我们需要求解 x 的值。解答:$3x\ =\ 639$$\Longrightarrow \ x\ =\ \frac{639}{3} \ =\ 213$$\Longrightarrow \ x\ =\ 213$
棉花的获取步骤如下:棉花以棉球的形式从棉花植物(陆地棉属植物)上手工采摘。通过轧棉机的过程,将种子和棉花纤维与棉花球分离。然后将这些棉花球制成线,并通过纺纱的过程转化为纱线。用这些纱线制成棉布。黄麻的获取步骤如下:黄麻纤维来自黄麻植物的茎和韧皮部(外皮)。纤维首先通过浸渍提取。浸渍过程包括将黄麻茎捆绑在一起并将其浸入缓慢流动的水中。然后…… 阅读更多
已知:给定的表达式为 $(7^2)^3 \times [(\frac{1}{7})^2]^3$。 求解:我们需要计算给定的表达式。解答:我们知道,$a^m \times a^n = a^{m+n}, (a^m)^n = a^{m\times n}$ 以及 $a^{-m} = \frac{1}{a^m}$$(7^2)^3 \times [(\frac{1}{7})^2]^3 = (7)^{2 \times 3} \times (\frac{1}{7})^{2\times 3}$ $= 7^6 \times (\frac{1}{7})^6$ $= 7^6 \times 7^{-6}$ $= (7)^{6+(-6)}$ $= (7)^{6-6}$ $ = 7^0$ $= 1$. (任何数的 0 次方等于 1)因此,$(7^2)^3 \times [(\frac{1}{7})^2]^3$ 的值为 1。
已知:给定的表达式为 $(\frac{5}{3})^4 \times (\frac{5}{3})^4 \div (\frac{5}{3})^2$。 求解:我们需要计算给定的表达式。解答:$(\frac{5}{3})^4 \times (\frac{5}{3})^4 \div (\frac{5}{3})^2$。我们知道,$a^m \times a^n = a^{m+n}$ 以及 $a^m \div a^n = a^{m-n}$ $(\frac{5}{3})^4 \times (\frac{5}{3})^4 \div (\frac{5}{3})^2 = (\frac{5}{3})^{4+4-2}$ $ = (\frac{5}{3})^{8-2}$ $ = (\frac{5}{3})^{6}$.因此,$(\frac{5}{3})^4 \times (\frac{5}{3})^4 \div (\frac{5}{3})^2$ 的值为 $(\frac{5}{3})^{6}$。
解答:凸多边形是一个简单多边形(不自交),其中边界上任意两点之间的线段永远不会在多边形外部。这也适用于四边形,因为它们也是四条边的多边形。矩形是四边形,因为它有四条边。矩形是凸四边形,因为边界上任意两点之间的线段都不会在矩形外部。矩形的任何对角线都不会在矩形外部。
已知:$-3a + 4b -5c$ 和 $8a + b -6c$ 求解:我们需要求解 $-3a + 4b -5c$ 比 $8a + b -6c$ 大多少。解答:$-3a + 4b -5c - ( 8a + b -6c)$ =$ -3a + 4b -5c -8a -b + 6c$ =$-11a + 3b + c$ 因此,$-3a + 4b -5c$ 比 $8a + b -6c$ 大 $-11a + 3b + c$。
已知:一个罐子里有 10 个红球和 8 个白球随机抽取一个球 求解:求抽到白球的概率。解答:红球数量 = 10 白球数量 = 8 可能事件总数 = 18 有利事件,即抽到白球的事件 = 8 所以抽到白球的概率 = $\frac{有利事件数}{可能事件总数}$ = $\frac{8}{18}$ = $\frac{4}{9}$ 答案因此,抽到白球的概率是 $\frac{4}{9}$
求解:化简表达式。解答: a) $\frac{2}{3} + \frac{1}{6}$ 3 和 6 的最小公倍数是 6 = $\frac{2\times2}{3\times2}$ + $\frac{1}{6}$ = $\frac{4}{6} + \frac{1}{6} =\frac{ 5}{6}$ 答案 b) $\frac{2}{3} - \frac{7}{16}$ 3 和 16 的最小公倍数是 48 $\frac{2\times16}{3\times16} - \frac{7\times3}{16\times3}$ = $\frac{32}{48} - \frac{21}{48} = \frac{32 - 21}{48}$ = $\frac{11}{48} $ 答案
已知:给定的数字是 0.0001。求解:我们需要找到用哪个小数除以 0.0001 可以得到 0.01。解答:我们知道,$\frac{a^m}{a^n} = a^{m-n}$ 令用以除以 0.0001 得到 0.01 的数字为 x。$0.0001 = 1 \times 10^{-4}$(小数点后有四位数字)$0.01 = 1 \times 10^{-2}$ (小数点后有两位数字) 因此,$\frac{0.0001}{x} = 0.01$$x = \frac{0.0001}{0.01}$$x =\frac{1 \times 10^{-4}}{1 \times 10^{-2}}$ $x = 10^{-4-(-2)}$ $x = 10^{-4+2}$ $x = 10^{-2}$ $x = 0.01$ 所需的小数是 0.01。

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP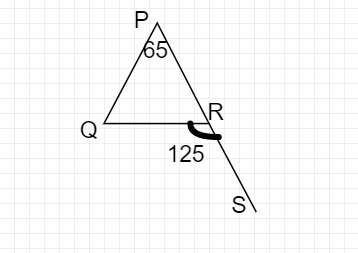 "\
"\