在给定的三角形 PQR 中，求角∠PRQ 和∠PQR。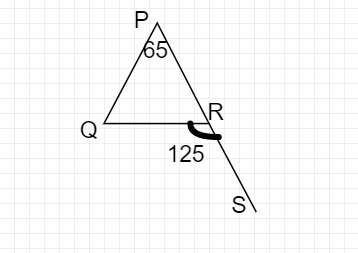"\n

已知：在三角形 PQR 中，∠QRS = 125°；∠QPR = 65°

求解：我们需要求出∠PRQ 和∠PQR。

解

∠PRQ 和∠QRS 构成一个线性对，因为它们是 R 点的内角和外角

∠PRQ + ∠QRS = 180°

∠PRQ + 125° = 180°；所以∠PRQ = 180° - 125° = 55°

根据三角形 PQR 的内角和性质。

∠PRQ + ∠PQR + ∠QPR = 180°；55° + ∠PQR + 65° = 180°；

∠PQR = 180° - 120° = 60°

所以∠PRQ = 55° 和∠PQR = 60°

教程点

更新于： 2022年10月10日

56 次浏览

开启你的职业生涯

通过完成课程获得认证

立即开始