连续整数

---

介绍

连续整数是指按照特定顺序或次序依次排列的整数。自然数、整数、有理数和无理数、实数和整数是一些数字类型。整数是包含所有正整数、负整数和零的集合。“整数”是一个拉丁词，意为完整或全部。这意味着分数或小数不包含在整数中。

• 例如，1、−5、4、9、−6。我们可以对整数进行基本的算术运算，即加法、减法、乘法和除法。连续整数是指按照特定模式或顺序依次排列的数字。连续整数之间的差值始终是常数。这些整数按升序排列。这个概念用于构建文字题。

整数

• 定义为包含所有整数、负数和零的集合。

• 正数、负数和零构成一组称为

• 它们用 Z 表示。

• 这些数字是整数，它们没有分数或小数部分。

• −5、0、8、−6、96、32 是一些整数的例子。

• 整数在数轴上表示。

• 正数标记在数轴的右侧。而负数标记在数轴的左侧。

• 零既不是正数也不是负数，因此它标记在数轴的中间。

• 这个点称为数轴的原点。

• 下图表示数轴上的整数。

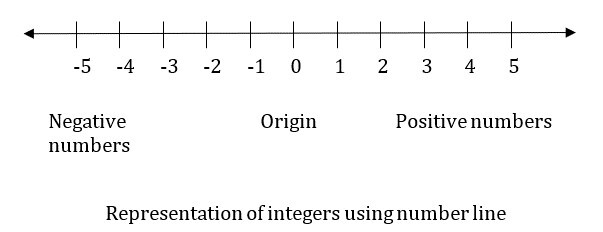
• 这些运算可以通过两种方式执行，要么使用代数规则，要么使用数轴。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

连续整数

• 连续整数是指按照特定顺序或模式依次排列的数字。

• 每个连续整数之间的差值是常数，即固定值。

• 例如，自然数集 1、2、3、4、5、6、……，在这里我们可以看到每个项之间的差值都是 1。

• 如果 n 是任何数字，则数字序列可以表示为 n+1、n+2、……、n+m，其中 m 表示序列中的最后一个数字。

• 这些数字按升序排列。

• 连续整数的一般公式为 n+1。

连续正数和负数

• 要找到连续整数的序列，第一个整数必须为正数或大于零才能获得一系列正数。

• 由于连续整数按升序排列，因此其他数字默认情况下将为正数。

• 此术语用于计数。

• 而要找到连续负整数的序列，第一个整数必须为负数或小于零才能获得一系列负数。

• 由于连续整数按升序排列，因此其他数字默认情况下将为负数。

连续偶数和奇数整数

连续偶数整数

• 偶数是 2 的倍数。连续偶数整数是一组偶数整数。

• 连续偶数整数之间的差值是 2。

• 假设 𝑧 是任何整数，则连续偶数整数可以写成 𝑧、𝑧 + 2、𝑧 + 4 等。

• 连续偶数整数的一般公式为 2n，其中 n 是任何整数。

连续奇数整数

• 奇数不是 2 的倍数。连续奇数整数是一组奇数整数。

• 连续奇数整数之间的差值是 2。

• 假设 z 是任何整数，则连续奇数整数可以写成 𝑧、𝑧 + 2、𝑧 + 4 等。

• 连续奇数整数的一般公式为 2n+1，其中 n 是任何整数。

两个连续整数的乘积（始终非负）

• 假设 m 和 n 是任何两个连续整数，并且 m 和 n 的乘积表示为

$$\mathrm{Product\:=\:m\times\:n}$$

• 例如，$\mathrm{2\times\:1\:=\:1}$

$\mathrm{--4\times\:-3\:=\:12}$

$\mathrm{-9\times\:-8\:=\:72}$

• 从以上示例可以看出，连续数字的乘积是 2 的倍数。

• 因此，连续数字的乘积是 2 的倍数，即偶数

• 此外，两个整数的乘积为正。

解题示例

1) 在序列 3、6、9、…、15、18、21、24 中找到缺失的数字？

答案 - 序列中连续数字之间的差值是 3。缺失数字的前一个数字是 9，后一个数字是 15。

缺失的数字 = 前一个数字 + 差值 = 9 + 3 = 12。

2) 如果三个连续数字的和为 51，则求出这三个连续数字？

答案 - 假设三个连续数字为 𝑛、𝑛 + 1 和 𝑛 + 2。

三个连续数字的和为 51

$$\mathrm{n\:+\:n\:+\:1\:+\:n\:2\:=\:51}$$

$$\mathrm{3n\:+\:3\:=\:51}$$

$$\mathrm{3n\:-\:51\:-\:3}$$

$$\mathrm{3n\:=\:48}$$

$$\mathrm{n\:=\:\frac{48}{3}}$$

$$\mathrm{n\:=\:16}$$

第一个连续数字是 16。

第二个数字 $\mathrm{=\:n\:+\:1\:=\:16\:+\:1\:=\:17}$

第三个数字 $\mathrm{=\:n\:+\:2\:=\:16\:+\:2\:=\:18}$

三个连续整数是 16、17 和 18。

3) 如果四个连续奇数整数的和为 112，则求出连续整数？

答案 - 两个连续奇数之间的差值为 2。假设第一个整数为 𝑛，第二个、第三个和第四个奇数整数将分别为 $\mathrm{n\:+\:2,n\:+\:4\&\:n\:+\:6}$。

已知四个连续整数的和为 112。

$$\mathrm{n\:+\:n\:+\:2\:+\:n\:+\:4\:+\:n\:+\:6\:=\:112}$$

$$\mathrm{4n\:+\:12\:=\:112}$$

$$\mathrm{4n\:=\:112\:-\:12}$$

$$\mathrm{4n\:=\:100}$$

$$\mathrm{n\:=\:\frac{100}{4}}$$

$$\mathrm{n\:=\:25}$$

其他整数将为

$$\mathrm{n\:+\:2\:=\:25\:+\:2\:=\:27}$$

$$\mathrm{n\:+\:4\:=\:25\:+\:4\:=\:29}$$

$$\mathrm{n\:+\:6\:=\:25\:+\:6\:=\:31}$$

四个连续奇数整数是 25、27、29 和 31。

结论

• 本教程简要介绍了连续整数的主题。

• 在本教程中，我们学习了整数、连续整数和两个整数的乘积，并提供了解题示例。

• 整数是正数、负数和零的集合。

• 它们是整数，没有分数或小数部分。

• 连续整数按照特定顺序或次序依次排列。

• 此外，我们还讨论了连续正数和负数整数以及连续偶数和奇数整数。

• 两个连续奇数和偶数整数之间的差值是 2。

常见问题解答

1. 判断以下陈述是真还是假，两个连续自然数的乘积始终为偶数？

正确

2. 什么是非连续整数？

它是一组整数，其中整数不是按顺序排列的。例如，2、5、10、21

3. 偶数个整数的乘积是否为正？

是。偶数个整数的乘积为正，奇数个整数的乘积为负。

4. 整数的加法单位是什么？

加法单位性质指出，当我们将零加到任何数字时，它会给出原始数字作为答案。零是整数的加法单位。

5. 连续数字的和是多少？

连续数字的和可以使用以下公式计算

$$\mathrm{\frac{n}{2}\times\:(第一个数字\:+\:最后一个数字)}$$