C语言实现的数据结构与算法 - 图

上一页
下一页

概述

图是一种用于模拟数学图的数据结构。它由一组称为顶点边的连接对组成。我们可以使用顶点数组和二维边数组来表示图。

重要术语

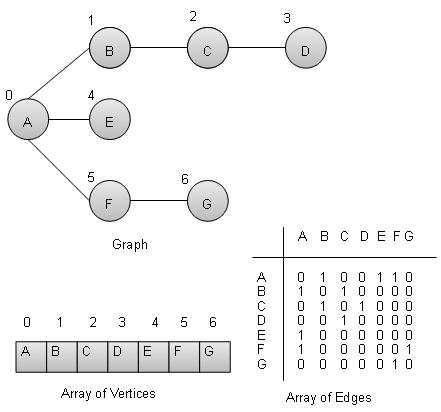
  • 顶点 − 图的每个节点都表示为一个顶点。在下面的示例中，带标签的圆圈表示顶点。因此，A到G是顶点。我们可以使用如下所示的数组来表示它们。这里A可以用索引0表示，B可以用索引1表示，以此类推。

  • 边 − 边表示两个顶点之间的路径或两点之间的线。在下面的示例中，从A到B、B到C等的线表示边。我们可以使用如下所示的二维数组来表示数组。这里AB可以在第0行，第1列表示为1，BC可以在第1行，第2列表示为1，以此类推，其他组合保持为0。

  • 邻接 − 如果两个节点或顶点通过一条边连接在一起，则它们是邻接的。在下面的示例中，B与A相邻，C与B相邻，以此类推。

  • 路径 − 路径表示两个顶点之间的一系列边。在下面的示例中，ABCD表示从A到D的路径。

Graph

基本操作

以下是图的基本主要操作。

  • 添加顶点 − 向图中添加一个顶点。

  • 添加边 − 在图的两个顶点之间添加一条边。

  • 显示顶点 − 显示图中的一个顶点。

添加顶点操作

//add vertex to the vertex list
void addVertex(char label){
struct vertex* vertex = 
   (struct vertex*) malloc(sizeof(struct vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}

添加边操作

//add edge to edge array
void addEdge(int start,int end){
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

显示边操作

//display the vertex
void displayVertex(int vertexIndex){
   printf("%c ",lstVertices[vertexIndex]->label);
}

遍历算法

以下是图上重要的遍历算法。

  • 深度优先搜索 − 深度遍历图。

  • 广度优先搜索 − 广度遍历图。

深度优先搜索算法

深度优先搜索算法(DFS)以深度优先的方式遍历图，并使用堆栈来记住当任何迭代中出现死胡同时要开始搜索的下一个顶点。

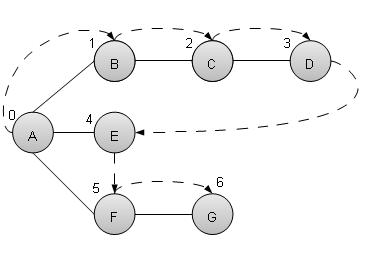
Depth First Search

如上例所示，DFS算法首先从A遍历到B到C到D，然后到E，然后到F，最后到G。它采用以下规则。

  • 规则1 − 访问相邻的未访问顶点。标记为已访问。显示它。将其压入堆栈。

  • 规则2 − 如果找不到相邻顶点，则从堆栈中弹出顶点。（它将弹出堆栈中所有没有相邻顶点的顶点。）

  • 规则3 − 重复规则1和规则2，直到堆栈为空。

void depthFirstSearch(){
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   
   //display the vertex
   displayVertex(0);   
   
   //push vertex index in stack
   push(0);

   while(!isStackEmpty()){
      //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
      
      //no adjacent vertex found
      if(unvisitedVertex == -1){
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }
   //stack is empty, search is complete, reset the visited flag        
   for(i=0;i < vertexCount;i++){
      lstVertices[i]->visited = false;
   }        
}

广度优先搜索算法

广度优先搜索算法(BFS)以广度优先的方式遍历图，并使用队列来记住当任何迭代中出现死胡同时要开始搜索的下一个顶点。

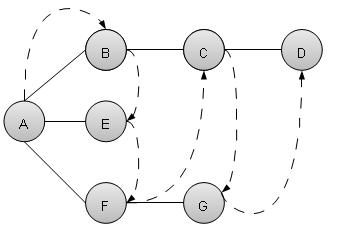
Breadth First Search

如上例所示，BFS算法首先从A遍历到B到E到F，然后到C和G，最后到D。它采用以下规则。

  • 规则1 − 访问相邻的未访问顶点。标记为已访问。显示它。将其插入队列。

  • 规则2 − 如果找不到相邻顶点，则从队列中删除第一个顶点。

  • 规则3 − 重复规则1和规则2，直到队列为空。

void breadthFirstSearch(){
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   
   //display the vertex
   displayVertex(0);   
   
   //insert vertex index in queue
   insert(0);
   int unvisitedVertex;
   while(!isQueueEmpty()){
      //get the unvisited vertex of vertex which is at front of the queue
      int tempVertex = removeData();         
      
      //no adjacent vertex found
      while((unvisitedVertex=getAdjUnvisitedVertex(tempVertex)) != -1){    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }
   } 
   //queue is empty, search is complete, reset the visited flag        
   for(i=0;i<vertexCount;i++){
      lstVertices[i]->visited = false;
   }    
}

示例

在线演示 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 10

struct Vertex {
   char label;
   bool visited;
};

//stack variables
int stack[MAX]; 
int top=-1; 

//queue variables
int queue[MAX];
int rear=-1;
int front=0;
int queueItemCount = 0;

//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];

//adjacency matrix
int adjMatrix[MAX][MAX];

//vertex count
int vertexCount = 0;

//stack functions
void push(int item) { 
   stack[++top]=item; 
}
int pop() { 
   return stack[top--]; 
} 
int peek() {         
   return stack[top];
}
bool isStackEmpty(){
   return top == -1;
}
//queue functions
void insert(int data){
   queue[++rear] = data;
   queueItemCount++;
}
int removeData(){
   queueItemCount--;
   return queue[front++]; 
}
bool isQueueEmpty(){
   return queueItemCount == 0;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label){
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end){
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex){
   printf("%c ",lstVertices[vertexIndex]->label);
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex){
   int i;
   for(i=0; i<vertexCount; i++)
      if(adjMatrix[vertexIndex][i]==1 && lstVertices[i]->visited==false)
         return i;
   return -1;
}
void depthFirstSearch(){
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   
   //display the vertex
   displayVertex(0);   
   
   //push vertex index in stack
   push(0);

   while(!isStackEmpty()){
      //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
      
      //no adjacent vertex found
      if(unvisitedVertex == -1){
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }
   //stack is empty, search is complete, reset the visited flag        
   for(i=0;i < vertexCount;i++){
      lstVertices[i]->visited = false;
   }        
}
void breadthFirstSearch(){
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   
   //display the vertex
   displayVertex(0);   
   
   //insert vertex index in queue
   insert(0);
   int unvisitedVertex;
   while(!isQueueEmpty()){
      //get the unvisited vertex of vertex which is at front of the queue
      int tempVertex = removeData();         
      
      //no adjacent vertex found
      while((unvisitedVertex=getAdjUnvisitedVertex(tempVertex)) != -1){    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }
   }
   //queue is empty, search is complete, reset the visited flag        
   for(i=0;i<vertexCount;i++){
      lstVertices[i]->visited = false;
   }    
}
main() {
   int i, j;
   
   for(i=0; i<MAX; i++) // set adjacency
      for(j=0; j<MAX; j++) // matrix to 0
         adjMatrix[i][j] = 0;

   addVertex('A');   //0
   addVertex('B');   //1
   addVertex('C');   //2
   addVertex('D');   //3
   addVertex('E');   //4
   addVertex('F');   //5
   addVertex('G');   //6

   /*      1  2  3   
   * 0  |--B--C--D
   * A--|
   * |
   * |     4 
   * |-----E
   * |     5  6
   * |  |--F--G
   * |--| 
   */        
   addEdge(0, 1);   //AB
   addEdge(1, 2);   //BC
   addEdge(2, 3);   //CD
   addEdge(0, 4);   //AC
   addEdge(0, 5);   //AF
   addEdge(5, 6);   //FG
   printf("Depth First Search: ");
   
   //A B C D E F G
   depthFirstSearch();              
   printf("\nBreadth First Search: ");
   
   //A B E F C G D
   breadthFirstSearch();
}

如果我们编译并运行上述程序，则将产生以下结果：

Depth First Search: A B C D E F G 
Breadth First Search: A B E F C G D
打印页面
上一页
下一页
广告