
- C语言数据结构教程
- C语言数据结构 - 首页
- C语言数据结构 - 概述
- C语言数据结构 - 环境搭建
- C语言数据结构 - 算法
- C语言数据结构 - 概念
- C语言数据结构 - 数组
- C语言数据结构 - 链表
- C语言数据结构 - 双向链表
- C语言数据结构 - 循环链表
- C语言数据结构 - 栈
- C语言数据结构 - 表达式解析
- C语言数据结构 - 队列
- C语言数据结构 - 优先队列
- C语言数据结构 - 树
- C语言数据结构 - 哈希表
- C语言数据结构 - 堆
- C语言数据结构 - 图
- C语言数据结构 - 搜索技术
- C语言数据结构 - 排序技术
- C语言数据结构 - 递归
- C语言数据结构 - 有用资源
- C语言数据结构 - 快速指南
- C语言数据结构 - 有用资源
- C语言数据结构 - 讨论
C语言数据结构 - 树
概述
树由节点和边连接而成。我们将专门讨论二叉树或二叉搜索树。
二叉树是一种特殊的数据结构,用于数据存储目的。二叉树有一个特殊的条件,即每个节点最多可以有两个子节点。二叉树结合了有序数组和链表的优点,搜索速度像有序数组一样快,插入或删除操作像链表一样快。
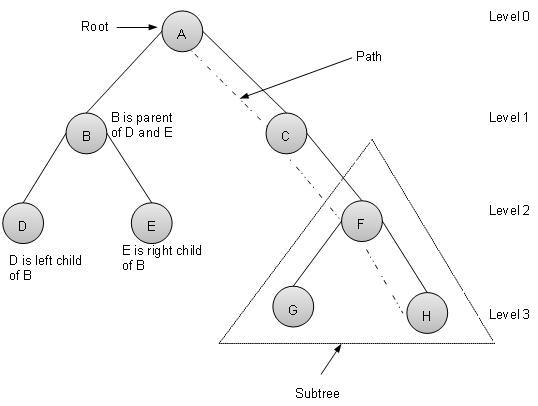
术语
以下是关于树的一些重要术语。
路径 - 路径指的是沿着树的边的一系列节点。
根节点 - 树顶部的节点称为根节点。每棵树只有一个根节点,并且从根节点到任何节点都只有一条路径。
父节点 - 除根节点之外的任何节点都有一条向上连接到称为父节点的节点的边。
子节点 - 下方通过边向下连接到给定节点的节点称为其子节点。
叶子节点 - 没有子节点的节点称为叶子节点。
子树 - 子树表示节点的后代。
访问 - 访问指的是当控制权在节点上时检查节点的值。
遍历 - 遍历意味着以特定顺序依次经过节点。
层级 - 节点的层级表示节点的代数。如果根节点在第 0 层,则其子节点在第 1 层,其孙子节点在第 2 层,依此类推。
键 - 键表示节点的值,根据该值执行节点的搜索操作。
二叉搜索树表现出特殊的行为。节点的左子节点的值必须小于其父节点的值,节点的右子节点的值必须大于其父节点的值。
二叉搜索树表示
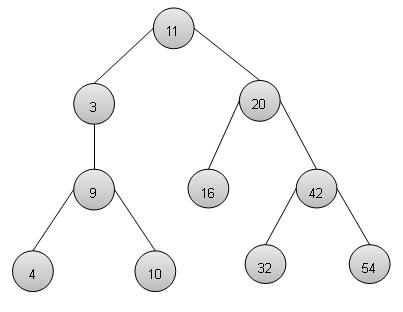
我们将使用节点对象来实现树,并通过引用将它们连接起来。
基本操作
以下是树的基本主要操作。
搜索 - 在树中搜索一个元素。
插入 - 在树中插入一个元素。
先序遍历 - 以先序方式遍历树。
中序遍历 - 以中序方式遍历树。
后序遍历 - 以后序方式遍历树。
节点
定义一个节点,它包含一些数据,以及指向其左右子节点的引用。
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
搜索操作
当要搜索一个元素时。从根节点开始搜索,如果数据小于键值,则在左子树中搜索元素,否则在右子树中搜索元素。对每个节点遵循相同的算法。
struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data){
if(current != NULL)
printf("%d ",current->data);
//go to left tree
if(current->data > data){
current = current->leftChild;
}//else go to right tree
else{
current = current->rightChild;
}
//not found
if(current == NULL){
return NULL;
}
}
return current;
}
插入操作
当要插入一个元素时。首先找到其合适的位置。从根节点开始搜索,如果数据小于键值,则在左子树中搜索空位置并插入数据。否则,在右子树中搜索空位置并插入数据。
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL){
root = tempNode;
} else {
current = root;
parent = NULL;
while(1){
parent = current;
//go to left of the tree
if(data < parent->data){
current = current->leftChild;
//insert to the left
if(current == NULL){
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else{
current = current->rightChild;
//insert to the right
if(current == NULL){
parent->rightChild = tempNode;
return;
}
}
}
}
}
先序遍历
这是一个简单的三步过程。
访问根节点
遍历左子树
遍历右子树
void preOrder(struct node* root){
if(root!=NULL){
printf("%d ",root->data);
preOrder(root->leftChild);
preOrder(root->rightChild);
}
}
中序遍历
这是一个简单的三步过程。
遍历左子树
访问根节点
遍历右子树
void inOrder(struct node* root){
if(root!=NULL){
inOrder(root->leftChild);
printf("%d ",root->data);
inOrder(root->rightChild);
}
}
后序遍历
这是一个简单的三步过程。
遍历左子树
遍历右子树
访问根节点
void postOrder(struct node* root){
if(root!=NULL){
postOrder(root->leftChild);
postOrder(root->rightChild);
printf("%d ",root->data);
}
}
示例
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL){
root = tempNode;
} else {
current = root;
parent = NULL;
while(1){
parent = current;
//go to left of the tree
if(data < parent->data){
current = current->leftChild;
//insert to the left
if(current == NULL){
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else{
current = current->rightChild;
//insert to the right
if(current == NULL){
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data){
if(current != NULL)
printf("%d ",current->data);
//go to left tree
if(current->data > data){
current = current->leftChild;
}//else go to right tree
else{
current = current->rightChild;
}
//not found
if(current == NULL){
return NULL;
}
}
return current;
}
void preOrder(struct node* root){
if(root!=NULL){
printf("%d ",root->data);
preOrder(root->leftChild);
preOrder(root->rightChild);
}
}
void inOrder(struct node* root){
if(root!=NULL){
inOrder(root->leftChild);
printf("%d ",root->data);
inOrder(root->rightChild);
}
}
void postOrder(struct node* root){
if(root!=NULL){
postOrder(root->leftChild);
postOrder(root->rightChild);
printf("%d ",root->data);
}
}
void traverse(int traversalType){
switch(traversalType){
case 1:
printf("\nPreorder traversal: ");
preOrder(root);
break;
case 2:
printf("\nInorder traversal: ");
inOrder(root);
break;
case 3:
printf("\nPostorder traversal: ");
postOrder(root);
break;
}
}
int main()
{
/* 11 //Level 0
*/
insert(11);
/* 11 //Level 0
* |
* |---20 //Level 1
*/
insert(20);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
*/
insert(3);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* |--42 //Level 2
*/
insert(42);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* |--42 //Level 2
* |
* |--54 //Level 3
*/
insert(54);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* 16--|--42 //Level 2
* |
* |--54 //Level 3
*/
insert(16);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* 16--|--42 //Level 2
* |
* 32--|--54 //Level 3
*/
insert(32);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* |
* 32--|--54 //Level 3
*/
insert(9);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* | |
* 4--| 32--|--54 //Level 3
*/
insert(4);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* | |
* 4--|--10 32--|--54 //Level 3
*/
insert(10);
struct node * temp = search(32);
if(temp!=NULL){
printf("Element found.\n");
printf("( %d )",temp->data);
printf("\n");
} else {
printf("Element not found.\n");
}
struct node *node1 = search(2);
if(node1!=NULL){
printf("Element found.\n");
printf("( %d )",node1->data);
printf("\n");
} else {
printf("Element not found.\n");
}
//pre-order traversal
//root, left ,right
traverse(1);
//in-order traversal
//left, root ,right
traverse(2);
//post order traversal
//left, right, root
traverse(3);
}
输出
如果我们编译并运行以上程序,它将产生以下输出:
Visiting elements: 11 20 42 Element found.(32) Visiting elements: 11 3 Element not found. Preorder traversal: 11 3 9 4 10 20 16 42 32 54 Inorder traversal: 3 4 9 10 11 16 20 32 42 54 Postorder traversal: 4 10 9 3 16 32 54 42 20 11