
- 使用 C 语言实现数据结构教程
- 使用 C 语言实现数据结构 - 首页
- 使用 C 语言实现数据结构 - 概述
- 使用 C 语言实现数据结构 - 环境
- 使用 C 语言实现数据结构 - 算法
- 使用 C 语言实现数据结构 - 概念
- 使用 C 语言实现数据结构 - 数组
- 使用 C 语言实现数据结构 - 链表
- 使用 C 语言实现数据结构 - 双向链表
- 使用 C 语言实现数据结构 - 循环链表
- 使用 C 语言实现数据结构 - 栈
- 使用 C 语言实现数据结构 - 表达式解析
- 使用 C 语言实现数据结构 - 队列
- 使用 C 语言实现数据结构 - 优先队列
- 使用 C 语言实现数据结构 - 树
- 使用 C 语言实现数据结构 - 哈希表
- 使用 C 语言实现数据结构 - 堆
- 使用 C 语言实现数据结构 - 图
- 使用 C 语言实现数据结构 - 搜索技术
- 使用 C 语言实现数据结构 - 排序技术
- 使用 C 语言实现数据结构 - 递归
- 使用 C 语言实现数据结构 - 有用资源
- 使用 C 语言实现数据结构 - 快速指南
- 使用 C 语言实现数据结构 - 有用资源
- 使用 C 语言实现数据结构 - 讨论
使用 C 语言实现数据结构 - 堆
概述
堆表示一种特殊的基于树的数据结构,用于表示优先队列或用于堆排序。我们将具体讨论二叉堆树。
二叉堆树可以归类为具有两个约束条件的二叉树:
完整性 - 二叉堆树是一个完整的二叉树,除了最后一层可能没有所有元素,但元素应从左到右填充。
堆特性 - 所有父节点都应大于或小于其子节点。如果父节点大于其子节点,则称为最大堆,否则称为最小堆。最大堆用于堆排序,最小堆用于优先队列。我们正在考虑最小堆,并将使用数组来实现它。
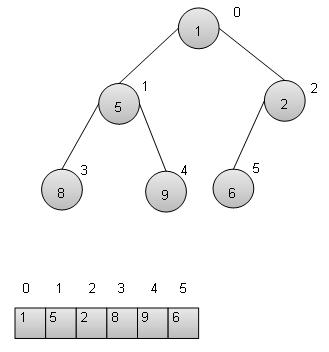
基本操作
以下是最小堆的基本主要操作:
插入 - 将元素插入堆中。
获取最小值 - 从堆中获取最小元素。
删除最小值 - 从堆中删除最小元素
插入操作
每当要插入元素时。将元素插入数组的末尾。将堆的大小增加 1。
当堆属性被破坏时,向上调整元素。将元素与其父节点的值进行比较,如果需要则交换它们。
void insert(int value) {
size++;
intArray[size - 1] = value;
heapUp(size - 1);
}
void heapUp(int nodeIndex){
int parentIndex, tmp;
if (nodeIndex != 0) {
parentIndex = getParentIndex(nodeIndex);
if (intArray[parentIndex] > intArray[nodeIndex]) {
tmp = intArray[parentIndex];
intArray[parentIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapUp(parentIndex);
}
}
}
获取最小值
获取实现堆的数组的第一个元素,即根节点。
int getMinimum(){
return intArray[0];
}
删除最小值
每当要删除元素时。获取数组的最后一个元素并将堆的大小减少 1。
当堆属性被破坏时,向下调整元素。将元素与其子节点的值进行比较,如果需要则交换它们。
void removeMin() {
intArray[0] = intArray[size - 1];
size--;
if (size > 0)
heapDown(0);
}
void heapDown(int nodeIndex){
int leftChildIndex, rightChildIndex, minIndex, tmp;
leftChildIndex = getLeftChildIndex(nodeIndex);
rightChildIndex = getRightChildIndex(nodeIndex);
if (rightChildIndex >= size) {
if (leftChildIndex >= size)
return;
else
minIndex = leftChildIndex;
} else {
if (intArray[leftChildIndex] <= intArray[rightChildIndex])
minIndex = leftChildIndex;
else
minIndex = rightChildIndex;
}
if (intArray[nodeIndex] > intArray[minIndex]) {
tmp = intArray[minIndex];
intArray[minIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapDown(minIndex);
}
}
示例
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
int intArray[10];
int size;
bool isEmpty(){
return size == 0;
}
int getMinimum(){
return intArray[0];
}
int getLeftChildIndex(int nodeIndex){
return 2*nodeIndex +1;
}
int getRightChildIndex(int nodeIndex){
return 2*nodeIndex +2;
}
int getParentIndex(int nodeIndex){
return (nodeIndex -1)/2;
}
bool isFull(){
return size == 10;
}
/**
* Heap up the new element,until heap property is broken.
* Steps:
* 1. Compare node's value with parent's value.
* 2. Swap them, If they are in wrong order.
* */
void heapUp(int nodeIndex){
int parentIndex, tmp;
if (nodeIndex != 0) {
parentIndex = getParentIndex(nodeIndex);
if (intArray[parentIndex] > intArray[nodeIndex]) {
tmp = intArray[parentIndex];
intArray[parentIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapUp(parentIndex);
}
}
}
/**
* Heap down the root element being least in value,until heap property is broken.
* Steps:
* 1.If current node has no children, done.
* 2.If current node has one children and heap property is broken,
* 3.Swap the current node and child node and heap down.
* 4.If current node has one children and heap property is broken, find smaller one
* 5.Swap the current node and child node and heap down.
* */
void heapDown(int nodeIndex){
int leftChildIndex, rightChildIndex, minIndex, tmp;
leftChildIndex = getLeftChildIndex(nodeIndex);
rightChildIndex = getRightChildIndex(nodeIndex);
if (rightChildIndex >= size) {
if (leftChildIndex >= size)
return;
else
minIndex = leftChildIndex;
} else {
if (intArray[leftChildIndex] <= intArray[rightChildIndex])
minIndex = leftChildIndex;
else
minIndex = rightChildIndex;
}
if (intArray[nodeIndex] > intArray[minIndex]) {
tmp = intArray[minIndex];
intArray[minIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapDown(minIndex);
}
}
void insert(int value) {
size++;
intArray[size - 1] = value;
heapUp(size - 1);
}
void removeMin() {
intArray[0] = intArray[size - 1];
size--;
if (size > 0)
heapDown(0);
}
main() {
/* 5 //Level 0
*
*/
insert(5);
/* 1 //Level 0
* |
* 5---| //Level 1
*/
insert(1);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
*/
insert(3);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* |
* 8--| //Level 2
*/
insert(8);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* |
* 8--|--9 //Level 2
*/
insert(9);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* | |
* 8--|--9 6--| //Level 2
*/
insert(6);
/* 1 //Level 0
* |
* 5---|---2 //Level 1
* | |
* 8--|--9 6--|--3 //Level 2
*/
insert(2);
printf("%d", getMinimum());
removeMin();
/* 2 //Level 0
* |
* 5---|---3 //Level 1
* | |
* 8--|--9 6--| //Level 2
*/
printf("\n%d", getMinimum());
}
如果我们编译并运行上述程序,它将产生以下结果:
1 2
广告