电力牵引：电车线垂度和张力的计算

电车线是指由大截面积的铜或铜合金制成的架空线，为电动车辆的电车提供所需的电流。

当一根柔性导线水平悬挂在两个电杆之间时，它会呈现悬链线的形状。但在有轨电车的情况下，电车线的垂度很少超过跨距长度的 1% 到 1.5%，因此可以认为电车线呈抛物线形状悬挂，如下图所示。

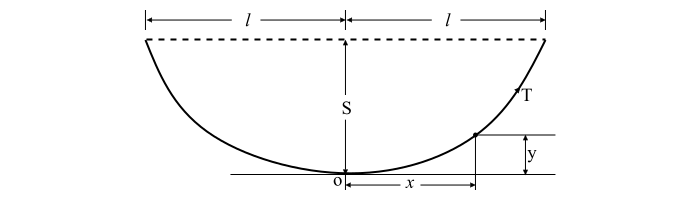
设：

$$\mathrm{电车线跨距长度（米）\, \mathrm{\: =\: }\, 2\mathit{l} }$$

$$\mathrm{导线单位长度重量（千克/米）\, \mathrm{\: =\: }\, \mathit{W}}$$

$$\mathrm{导线张力（千克）\, \mathrm{\: =\: }\, \mathit{T}}$$

然后，取支点力矩，我们有：

$$\mathrm{\mathit{TS\, \mathrm{\: =\: }\,Wl\times \left ( \frac{l}{\mathrm{2}} \right )} }$$

其中，S 为电车线的垂度。

$$\mathrm{\therefore 垂度,\mathit{S\, \mathrm{\: =\: }\, \frac{Wl^{\mathrm{2}}}{\mathrm{2}T}} \: \: \: \cdot \cdot \cdot \left ( 1 \right )}$$

现在，**所需导线长度的计算方法如下**：

由于抛物线的方程由以下表达式给出：

$$\mathrm{\mathit{y\, \mathrm{\: =\: }\, \frac{Sx^{\mathrm{2}}}{l^{\mathrm{2}}}}}$$

将式 (1) 中的 δ 的值代入，得到：

$$\mathrm{\mathit{y\, \mathrm{\: =\: }\, \frac{Wx^{\mathrm{2}}}{\mathrm{2}T}} \: \: \: \cdot \cdot \cdot \left ( 2 \right )}$$

由于：

$$\mathrm{\mathit{\frac{ds}{dx}\mathrm{\: =\: }\sqrt{\mathrm{1}\mathrm{\: +\: }\left ( \frac{dy}{dx} \right )^{\mathrm{2}}}}}$$

$$\mathrm{\left ( \because \mathit{\frac{dy}{dx}\mathrm{\: =\: }\frac{Wx}{T}} \right )}$$

$$\mathrm{\therefore \mathit{\frac{ds}{dx}\mathrm{\: =\: }\sqrt{\mathrm{1\mathrm{\: +\: }}\left ( \frac{Wx}{T} \right )^{\mathrm{2}}}}}$$

$$\mathrm{\Rightarrow \int \mathit{ds\mathrm{\: =\: }\int \sqrt{\mathrm{1}\mathrm{\: +\: }\left ( \frac{Wx}{T} \right )^{\mathrm{2}}}dx\mathrm{\: =\: }\int \left [ \mathrm{1}\mathrm{\: +\: }\frac{W^{\mathrm{2}}x^{\mathrm{2}}}{T^{\mathrm{2}}} \right ]^{\mathrm{1/2}}dx}}$$

$$\mathrm{\Rightarrow\mathit{s\mathrm{\: =\: }\int \left ( \mathrm{1}\mathrm{\: +\: }\frac{W^{\mathrm{2}}x^{\mathrm{2}}}{\mathrm{2}T^{\mathrm{2}}}\mathrm{\: +\: }\frac{\mathrm{3}W^{\mathrm{4}x^{\mathrm{4}}}}{\mathrm{8}T^{\mathrm{4}}}\mathrm{\: +\: }\cdot \cdot \cdot \right )dx}}$$

$$\mathrm{\therefore \mathit{s\mathrm{\: =\: }x\mathrm{\: +\: }\frac{W^{\mathrm{2}}x^{\mathrm{3}}}{\mathrm{6}T^{\mathrm{2}}}\mathrm{\: +\: }\cdot \cdot \cdot }$$

现在，当 𝑥 = 1，即跨距长度的一半时，跨距一半的导线长度由下式给出：

$$\mathrm{\mathit{s\mathrm{\: =\: }l\mathrm{\: +\: }\frac{W^{\mathrm{2}}l^{\mathrm{3}}}{\mathrm{6}T^{\mathrm{2}}}\mathrm{\: =\: }l\mathrm{\: +\: }\left ( \frac{\mathrm{2}TS}{l^{\mathrm{2}}} \right )^{\mathrm{2}}\times \left ( \frac{l^{\mathrm{3}}}{\mathrm{6}T^{\mathrm{2}}} \right )}}$$

$$\mathrm{\mathit{\Rightarrow s\mathrm{\: =\: }l\mathrm{\: +\: }\frac{\mathrm{2}S^{\mathrm{2}}}{\mathrm{3}l}}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

因此，整个跨距长度所需的导线总长度为

$$\mathrm{2\mathit{s\mathrm{\: =\: }\mathrm{2}\left [ l\mathrm{\: +\: }\frac{\mathrm{2}S^{\mathrm{2}}}{\mathrm{3}l} \right ]}\: \: \cdot \cdot \cdot \left ( 4 \right )}$$

此外，导线的长度会随着温度的变化而变化，这会导致给定跨距的垂度和张力发生变化。这里需要注意的是，温度降低会降低垂度并增加张力。

数值示例

一条有轨电车的电车线悬挂在两个相距 50 米的电杆之间。如果导线的直径为 2 厘米，单位长度重量为 1 千克，则在施加 650 千克的张力时，求其垂度。并求所需导线的总长度。

解答

已知数据：

$$\mathrm{跨距长度,\, 2\mathit{l}\mathrm{\: =\: }50\, m}$$

$$\mathrm{半跨距长度,\mathit{l}\mathrm{\: =\: }25\, m}$$

$$\mathrm{导线单位长度重量,\mathit{W}\mathrm{\: =\: }1\, kg}$$

$$\mathrm{施加张力,\mathit{T}\mathrm{\: =\: }650\, kg}$$

因此，导线的垂度为：

$$\mathrm{垂度, \mathit{S\mathrm{\: =\: }\frac{Wl^{\mathrm{2}}}{\mathrm{2}T}}\mathrm{\: =\: }\frac{1\times 25^{2}}{2\times 650}\mathrm{\: =\: }0.481\, m}$$

同样，所需导线的总长度为：

$$\mathrm{2\mathit{s\mathrm{\: =\: }\mathrm{2}\left [ l\mathrm{\: +\: }\frac{\mathrm{2}S^{\mathrm{2}}}{\mathrm{3}l} \right ]}\mathrm{\: =\: }2\times \left [ 25\mathrm{\: +\: }\frac{2}{3}\times \frac{0.481^{2}}{25} \right ]\mathrm{\: =\: }50.0123 \, m}$$

Manish Kumar Saini

更新于： 2022年5月19日

812 次查看

开启您的 职业生涯

通过完成课程获得认证

立即开始