数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在计算理论（TOC）中，使用框图解释 DFA 的工作原理。
在计算理论（TOC）中，有限自动机（FA）表示如下：
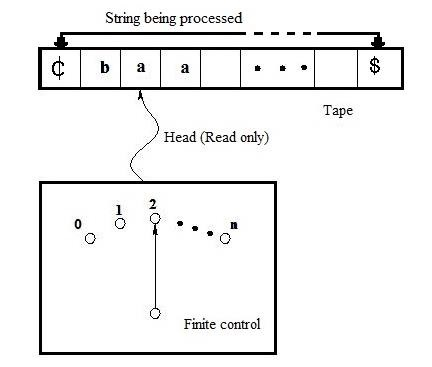
FA 的组成部分
有限自动机的不同组成部分如下：
输入带
输入带具有左端并延伸到右端。
它被分成多个块，每个块包含来自输入字母表 Σ 的单个符号。
磁带的结束块在左端包含结束标记 ₵，在右端包含结束标记 $。
缺少结束标记表示磁带是无限长的。
两个结束标记之间从左到右的符号序列是待处理的输入字符串。
只读磁头
磁带有一个只读磁头，它一次检查一个块，并且可以向左或向右移动一个块。
在操作开始时，磁头始终位于输入磁带的最左端块。
然后机器仅限制只读磁头从左到右的方向移动，并且每次读取符号时都移动一个块。
有限控制
有一个有限控制确定自动机的状态，并控制磁头的移动。
有限控制的输入通常是读写磁头下的符号（假设为 a）和机器的当前状态（假设为 q），以给出以下输出；
沿着磁带到下一个块的读写磁头运动。
由 δ(q, a) 给出的有限状态机的下一个状态。
有限自动机的操作
有限自动机或确定性自动机在初始时间，假设机器处于初始状态 q0，其输入机制位于输入磁带中输入字符串的最左端符号上。
在自动机的每次移动过程中，输入机制向右移动一个位置，因此每次移动消耗一个输入符号。
当字符串到达末尾时，如果自动机处于其最终状态之一，则接受该字符串。否则，它被拒绝。
输入机制只能从左到右移动，并且在每个步骤中只读取一个符号。
从一个内部状态到另一个内部状态的转换受转换函数 δ 控制。
例如，如果 δ(q0, a) = q1，
那么，如果有限自动机处于状态 q0 且当前输入符号为 a，则机器将进入下一个状态 q1。
一旦到达状态 q1，无论读取什么符号，此机器都不会离开状态 q1，直到扫描或接受另一个输入符号。
示例
如果机器 M 定义为，请检查字符串 s = {01} 是否被机器接受。
M = ({q0, q1, q2}, {0, 1}, δ, q0{q1})，其中 δ 给定为；
δ (q0, 0) = q0，
δ (q0, 1) = q1，
δ (q1, 0) = q0，
δ (q1, 1) = q2，
δ (q2, 0) = q2，
δ (q2, 0) = q1。
此机器 M 接受字符串 01。让我们从状态 q0 开始，首先从输入磁带扫描符号 0。
查看图的边，很明显自动机保持在状态 q0。接下来，只读磁头升级 1 并读取 1，自动机进入状态 q1。
我们现在位于字符串的末尾，同时处于最终状态 q1。
1K+ 次查看
