解释 DFA 中的并集过程

下面解释了确定性有限自动机 (DFA) 中的并集过程。

如果 L1 和 L2 是两个正则语言，则它们的并集 L1 U L2 也将是正则的。

例如，

L1 = {an | n > O} 和 L2 = {bn | n > O}

L3 = L1 U L2 = {an U bn | n > O} 也是正则的。

问题

设计一个在字母表 {a,b} 上的 DFA，其中开始和结束符号不同。

解决方案

对于给定的条件，形成了两种不同类型的语言：

  • L1={ab,aab,abab,abb,…….}
  • L1={ab,aab,abab,abb,…….}

这里，

  • L1= 以 a 开头，以 b 结尾
  • L2= 以 b 开头，以 a 结尾

因此，

L=L1 U L2

或者

L=L1+L2

L1 的状态转换图

语言 L1 的状态转换图如下所示：

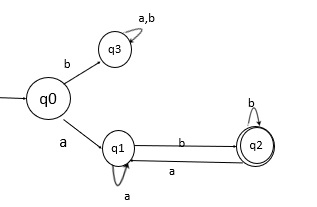
上述 DFA 接受所有以 a 开头并以 b 结尾的字符串。

这里，

  • q0 是初始状态。
  • q1 是中间状态。
  • q2 是最终状态。
  • q3 是死状态。

L2 的状态转换图

语言 L2 的状态转换图如下所示：

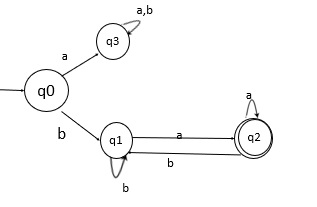
上述 DFA 接受所有以 b 开头并以 a 结尾的字符串。

这里，

  • q0：初始状态。
  • q1：中间状态。
  • q2：最终状态。
  • q3：死状态。

现在，L1 和 L2 的并集给出了语言的最终结果，该语言以不同的元素开头和结尾。

L1 U L2 的状态转换图 如下所示：

更新于： 2021年6月15日

3K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

立即开始
广告