数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究解释 DFA 中的补集过程
下面解释了确定性有限自动机 (DFA) 中的补集过程。
让我们以一个由 (Q, Σ, δ,q0,F) 定义的 DFA 为例，它接受语言 L1。现在，接受语言 L2 的 DFA，其中 L2 = ̅L1，定义如下：
(Q, Σ, δ,q0,Q-F)
DFA 的补集是通过将非终结状态设为终结状态，并将终结状态设为非终结状态得到的。
被补集 DFA L2 接受的语言是语言 L1 的补集。
示例
让我们考虑一些示例，以清楚地了解 DFA 的补集过程。
示例 1
考虑两种语言 L1 和 L2。
在 L1 中，所有字符串在字母表 {a,b} 上以 'a' 开头
L1={a,ab,aa,aba,aab,aaa,……}
在 L2 中，所有字符串在字母表 {a,b} 上不以 'a' 开头
L2={€, b,ba,bab,baa,bba,……}
在这里，我们可以观察到这两种语言的形式为：
L2 = ̅L1
下面给出了接受所有以 'a' 开头的 {a, b} 上的字符串集的 L1 的 DFA 的状态转换图：
q0 在 'a' 上转到 q1，q1 是一个终结状态，并生成以字母 'a' 开头的字符串
{a,ab,aab,abb,aaab,……}
其中 q2 是死状态。
构建补集的 DFA
现在，我们可以通过简单地交换终结状态和非终结状态来构建补集的 DFA。
这指的是将非终结状态更改为终结状态，并将终结状态更改为非终结状态。
构建补集的 DFA 后的状态转换图如下：
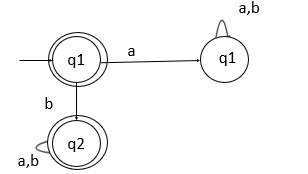
以上状态转换图是补集 DFA，它接受不以 'a' 开头的字符串。
q0 在 'a' 上转到 q1，q1 是一个死状态，因此，可以清楚地看到以上状态转换 DFA 不会生成以 'a' 开头的字符串。
更新于: 2021 年 6 月 15 日
1K+ 次查看
广告