使用 Python 中的 NumPy 生成具有给定根的 Hermite_e 级数

---

厄米特多项式是一组正交多项式，在各种数学应用中非常有用。它们常用于求解微分方程、概率论和量子力学。Hermite_e 级数是厄米特多项式的变体，用于根据其根表示函数。在本文中，我们将讨论如何使用 Python 中的 NumPy 生成具有给定根的 Hermite_e 级数。

安装和语法

NumPy 是一个 Python 库，它提供对数值运算的支持，可以使用 pip 安装，并使用语句“import numpy”导入到 Python 中。

pip install numpy

要使用 NumPy 生成具有给定根的 Hermite_e 级数，可以使用以下语法：

numpy.polynomial.hermite_e.hermegauss(roots, deg)

roots − 包含 Hermite_e 级数根的 1 维数组。

deg − Hermite_e 级数的次数。

算法

以下是使用 NumPy 生成具有给定根的 Hermite_e 级数的算法：

• 导入 NumPy 库。

• 定义一个包含 Hermite_e 级数根的数组。

• 定义 Hermite_e 级数的次数。

• 使用根和次数作为参数调用 numpy.polynomial.hermite_e.hermegauss() 函数。

• 该函数返回两个数组，一个包含 Hermite_e 级数的权重，另一个包含节点。

• 使用权重和节点构建 Hermite_e 级数。

示例 1

以下代码示例生成一个具有根 [-1, 0, 1] 和次数 2 的 Hermite_e 级数。

import numpy as np
roots = np.array([-1, 0, 1])
deg = 2
weights, nodes = np.polynomial.hermite_e.hermegauss(deg)
print(weights)
print(nodes)

输出

[-1.  1.]
[1.25331414 1.25331414]

示例 2

以下代码示例生成一个具有根 [1, 2, 3, 4] 和次数 3 的 Hermite_e 级数。

import numpy as np

# array of roots
roots = np.array([0, 1, 2, 3])

# initialize coefficients array with zeros
coeffs = np.zeros((len(roots), 2 * len(roots) - 1))

# setting up initial values of coefficients
coeffs[:, 0] = roots # setting f(x) values to be the roots
coeffs[1:, 1] = np.diff(coeffs[:, 0]) / np.diff(roots) # setting f'(x) values using finite difference method

# setting up the remaining coefficients using recurrence relation
for j in range(2, 2 * len(roots)):
   for i in range(len(roots)):
      if j % 2 == 0 and i >= j // 2:
         # even-indexed coefficients
         coeffs[i, j // 2] = coeffs[i, j // 2 - 1] * (j - 1) / (j // 2)
      elif j % 2 == 1 and i >= (j + 1) // 2:
         # odd-indexed coefficients
         coeffs[i, (j + 1) // 2 - 1] = (coeffs[i, j // 2] - coeffs[i - 1, j // 2]) / (roots[i] - roots[i - j // 2])

# generating the Hermite series using the calculated coefficients
def hermite_e_series(x):
   res = np.zeros_like(x)
   for i in range(len(roots)):
      term = np.ones_like(x)
      for j in range(i):
         term *= (x - roots[j])
      res += coeffs[i, i] * term
   return res
 

x = np.linspace(-1, 4, 1000)
y = hermite_e_series(x)

# get the first 10 coefficients
print(y[:10])

# plot the function
import matplotlib.pyplot as plt
plt.plot(x, y)
plt.show()

输出

[-5.5  -5.44884884 -5.39799735 -5.34744457 -5.29718957 -5.24723141                                                                                                       
 -5.19756916 -5.14820186 -5.09912858 -5.05034838]

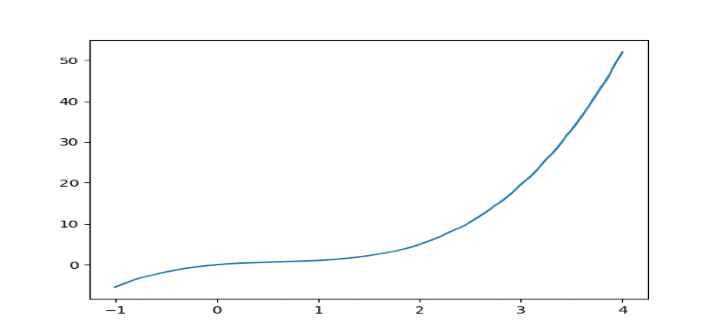
以下代码示例生成一个具有根 [0, 1, 2, 3] 和次数 4 的 Hermite_e 级数，并使用 Matplotlib 绘制该级数。

应用

在 Python 中使用 NumPy 生成的厄米特级数具有各种应用。在物理学中，厄米特多项式用于描述量子谐振子的波函数，同时在数值分析和科学计算中也证明非常有用，以及在统计学中实现近似函数（如正态分布），因为它通常以高精度实现近似函数。

结论

Hermite_e 级数是科学计算和数值分析中一个强大的工具。借助 Python 中的 NumPy，生成厄米特级数已成为一项简单的任务。生成该级数的算法包括设置初始系数，然后使用递推关系确定其余系数。一旦计算出系数，就可以使用简单函数生成厄米特级数。该级数在物理学、数学和统计学中具有众多应用。通过使用 Hermite_e 级数，科学家和数学家可以高精度地逼近复杂函数，使其成为许多研究领域的宝贵工具。