Python中的逆伽马分布

---

简介

逆伽马分布是一种连续概率分布，在贝叶斯统计、经济学和物理学等许多学科中出现。它作为正态分布中精度参数的共轭先验，并且常用于表示具有正偏度的变量。本文涵盖了逆伽马分布、其描述、Python中的语法以及带有工作代码的示例，以演示如何使用它。

逆伽马分布

定义

逆伽马分布是在正实数线上定义的概率分布。它由两个参数描述：形状（alpha）和尺度（beta）。逆伽马分布的概率密度函数（PDF）由以下公式给出：

f(x|alpha, beta) = (betaalpha / math.gamma(alpha)) * x(-alpha-1) * exp(-beta / x)

其中 x > 0，alpha > 0，beta > 0，并且 math.gamma 表示伽马函数。

语法

可以使用 Python 中的 scipy.stats 模块来处理逆伽马分布，该模块提供了大量概率分布。以下是构建逆伽马分布对象的语法：

from scipy.stats import invgamma
# Creating an Inverse Gamma distribution object
inverse_gamma_dist = invgamma(alpha, scale=beta)

您可以复制上述代码片段并将 alpha 和 beta 更改为逆伽马分布的形状和尺度参数的所需值。请注意，使用逆伽马分布需要在您的 Python 环境中安装 scipy.stats 模块。

语法解释

• ‘from scipy.stats import invgamma’：此行导入 scipy.stats 模块的 invgamma 类。

• ‘inverse_gamma_dist = invgamma(alpha, scale=beta)’：在此行中，alpha 用作形状参数，beta 用作尺度参数，以生成逆伽马分布的实例。

算法

• 步骤 1 - 导入所需的库

• 步骤 2 - 定义形状和尺度参数

• 步骤 3 - 创建一个逆伽马分布对象

• 步骤 4 - 从逆伽马分布生成随机数

• 步骤 5 - 绘制生成的数字的概率密度函数（PDF）和直方图

方法

• 方法 1 - 生成随机数

• 方法 2 - 概率密度函数（PDF）

方法 1：生成随机数

在此方法中，我们使用逆伽马分布对象的 rvs 方法从逆伽马分布生成随机数。我们可以通过选择 size 参数来控制生成的随机数的数量。

示例

import numpy as np
from scipy.stats import invgamma

# Define the shape and scale parameters
alpha = 3
beta = 2

# Create an Inverse Gamma distribution object
inverse_gamma_dist = invgamma(alpha, scale=beta)

# Generate random numbers from the Inverse Gamma distribution
random_numbers = inverse_gamma_dist.rvs(size=1000)

print(random_numbers)

输出

[0.50492148 0.99333748 1.75490027 ... 0.65061424 0.70721182 0.78544613]

方法 1 的主要目标是使用逆伽马分布生成随机数。逆伽马分布对象的 rvs 方法可用于快速生成所需数量的随机样本。在此方法中，我们首先指定逆伽马分布的形状 (alpha) 和尺度 (beta) 参数。接下来，我们使用 scipy.stats 模块中的 invgamma 类生成逆伽马分布的实例。通过在分布对象上使用 rvs 方法并提供所需的 size，使用逆伽马分布生成一组随机数。使用此方法，可以生成随机数来模拟数据或为各种目的运行蒙特卡罗模拟。

请注意，由于生成的随机数是随机生成的，因此每次运行代码时它们都会有所不同。

方法 2：概率密度函数（PDF）

在此方法中，我们使用逆伽马分布对象的 pdf 方法来可视化分布的概率密度函数（PDF）。这使我们能够看到分布的形状并理解其属性。

示例

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import invgamma

# Define the shape and scale parameters
alpha = 2.5
beta = 1.2

# Create an Inverse Gamma distribution object
inverse_gamma_dist = invgamma(alpha, scale=beta)

# Generate an array of x values
x = np.linspace(0.001, 10, 100)

# Calculate the PDF values for the x values
pdf_values = inverse_gamma_dist.pdf(x)

# Plot the PDF of the Inverse Gamma distribution
plt.plot(x, pdf_values, 'r-', label='PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('PDF of Inverse Gamma Distribution')
plt.legend()
plt.show()

输出

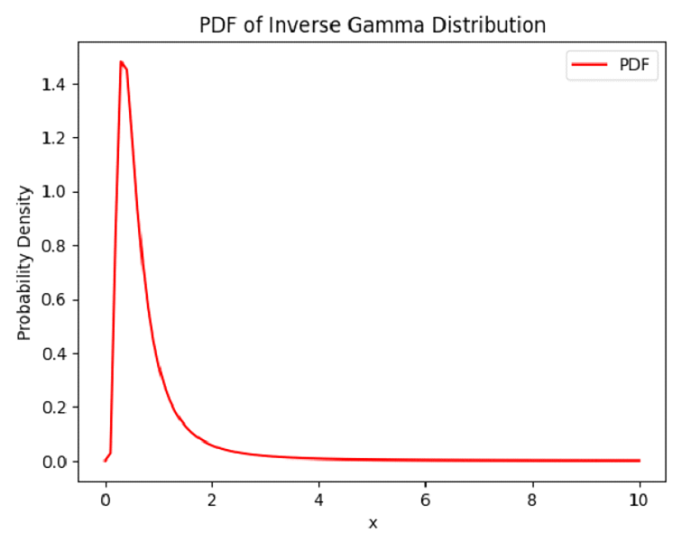
在此方法中，我们首先使用 np.linspace 函数生成一个从 0.001 到 10 之间 100 个均匀间隔的值的数组。这些 x 值表示我们想要评估 PDF 的范围。然后，使用逆伽马分布对象的 pdf 方法计算生成 x 值的概率密度函数（PDF）值。结果，我们得到每个 x 值的 PDF 值数组。

最后，我们使用 matplotlib.pyplot 模块的 plt.plot 方法绘制逆伽马分布的 PDF。生成的绘图在 x 轴上显示 x 值，在 y 轴上显示 PDF 值，从而显示分布的形状。通过可视化 PDF，我们可以看到重要的细节，如分布的位置、散布和偏度。使用此方法可以更好地理解逆伽马分布及其行为。

请注意，当您运行代码时，生成的绘图将显示在单独的窗口中。

结论

逆伽马分布是一种灵活的概率分布，应用于许多不同的领域。在本文中，我们讨论了其描述、Python 语法以及带有工作代码的示例，以演示如何使用它。通过掌握基础知识并利用 scipy.stats 模块，您可以使用逆伽马分布在 Python 中对数据建模和分析。逆伽马分布有许多应用，包括贝叶斯分析、金融和物理学。它提供了一种通用且有效的方法来对具有正偏度的变量建模。通过利用本文中提供的概念和示例，您可以自信地将逆伽马分布添加到您的 Python 数据分析项目中。

无论您需要生成随机数还是检查分布的特性，Python 和 scipy.stats 模块都提供了处理逆伽马分布所需的所有工具。