回归技术

---

---

回归是一种统计技术，有助于量化相互关联的经济变量之间的关系。第一步包括估计自变量的系数，然后衡量估计系数的可靠性。这需要制定假设，并根据假设，我们可以创建一个函数。

如果管理者想要确定公司广告支出与其销售收入之间的关系，他将进行假设检验。假设更高的广告支出导致公司更高的销售额。管理者收集特定时期广告支出和销售收入的数据。这个假设可以转化为数学函数，从而导致：

Y = A + Bx

其中Y是销售额，x是广告支出，A和B是常数。

在将假设转化为函数之后，其基础是找到因变量和自变量之间的关系。因变量的值对研究人员来说最为重要，并且取决于其他变量的值。自变量用于解释因变量的变化。它可以分为两种类型：

• 简单回归 - 一个自变量

• 多元回归 - 几个自变量

简单回归

建立回归分析的步骤如下：

• 指定回归模型
• 获取变量数据
• 估计定量关系
• 检验结果的统计显著性
• 将结果用于决策

简单回归公式为：

Y = a + bX + u

Y= 因变量

X= 自变量

a= 截距

b= 斜率

u= 随机因素

横截面数据提供关于给定时间一组实体的信息，而时间序列数据提供关于一个实体随时间推移的信息。当我们估计回归方程时，它涉及找到因变量和自变量之间最佳线性关系的过程。

普通最小二乘法 (OLS)

普通最小二乘法旨在通过散点拟合一条线，使得点到线的平方偏差之和最小化。这是一种统计方法。通常软件包执行 OLS 估计。

Y = a + bX

决定系数 (R²)

决定系数是一个衡量指标，它指示因变量变化的百分比是由自变量的变化引起的。R²是模型拟合优度的度量。方法如下：

总平方和 (TSS)

Y 的样本值与其平均值 Y 的平方偏差之和。

TSS = SUM ( Y_i − Y)²

Y_i = 因变量

Y = 因变量的平均值

i = 观察次数

回归平方和 (RSS)

Y 的估计值与其平均值 Y 的平方偏差之和。

RSS = SUM ( Ỷ_i − uY)²

Ỷ_i = Y 的估计值

Y = 因变量的平均值

i = 变异数

误差平方和 (ESS)

Y 的样本值与其估计值 Y 的平方偏差之和。

ESS = SUM ( Y_i − Ỷ_i)²

Ỷ_i = Y 的估计值

Y_i = 因变量

i = 观察次数

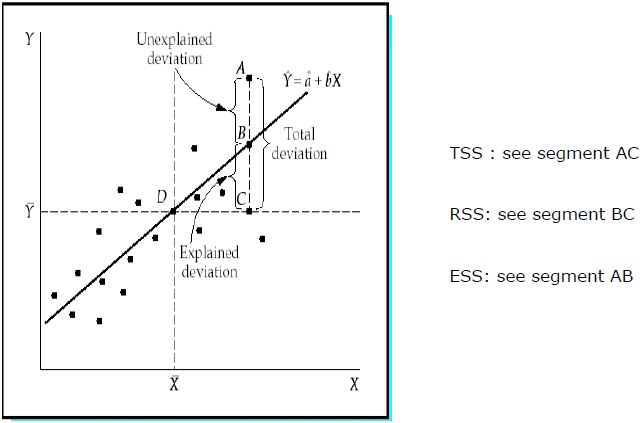
R²衡量的是由回归模型解释的 Y 与其平均值总偏差的比例。R²越接近于 1，回归方程的解释力就越大。接近 0 的 R² 表明回归方程的解释力非常小。

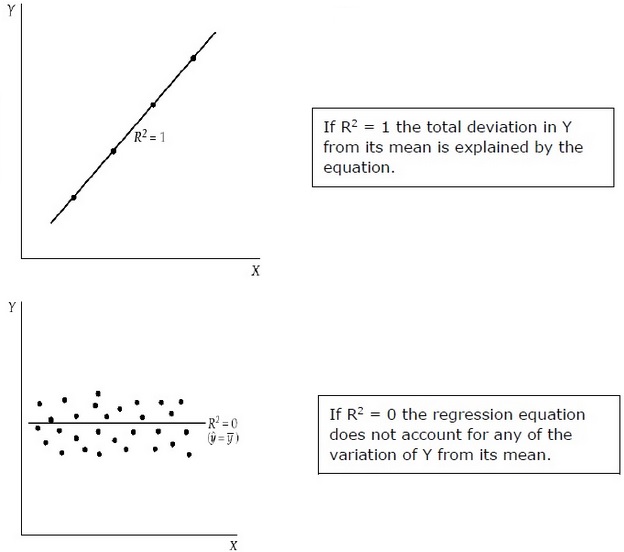
为了评估回归系数，使用的是来自总体的一个样本，而不是整个总体。重要的是要根据样本对总体做出假设，并判断这些假设有多好。

评估回归系数

来自总体的每个样本都会产生其自身的截距。为了计算统计差异，可以使用以下方法：

双尾检验：

零假设：H₀: b = 0

备择假设：H_a: b ≠ 0

单尾检验：

零假设：H₀: b > 0 (或 b < 0)

备择假设：H_a: b < 0 (或 b > 0)

统计检验：

b = 估计系数

E (b) = b = 0 (零假设)

SE_b = 系数的标准误

.

t的值取决于自由度、单尾或双尾检验以及显著性水平。可以使用 t 表来确定t的临界值。然后将 t 值与临界值进行比较。如果统计检验的绝对值大于或等于临界 t 值，则需要拒绝零假设。如果统计检验的绝对值小于临界 t 值，则不拒绝零假设。

多元回归分析

与简单回归不同，在多元回归分析中，系数表示假设其他变量的值保持不变时因变量的变化。

统计显著性检验称为F 检验。F 检验很有用，因为它衡量的是整个回归方程的统计显著性，而不仅仅是一个单独的变量。在这里，零假设是因变量与总体的自变量之间没有关系。

公式为：H₀: b1 = b2 = b3 = …. = bk = 0

对于总体，因变量与k个自变量之间不存在关系。

F 检验统计量：

$$F \: =\: \frac{ \left ( \frac{R^2}{K} \right )}{\frac{(1-R^2)}{(n-k-1)}}$$

F的临界值取决于分子和分母自由度以及显著性水平。可以使用 F 表来确定临界 F 值。将 F 值与临界值 (F*) 进行比较：

如果 F > F*，则需要拒绝零假设。

如果 F < F*，则不拒绝零假设，因为因变量与所有自变量之间没有显著关系。