
微波工程 - E-H 面T 型接头
E-H 面 T 型接头是由将两个简单的波导(一个平行,另一个串联)连接到已经具有两个端口的矩形波导而形成的。这也被称为魔T、混合器或3dB 耦合器。
矩形波导的臂形成两个称为共线端口的端口,即端口 1 和端口 2,而端口 3 称为H 臂或和端口或并联端口。端口 4 称为E 臂或差端口或串联端口。
可以通过下图了解魔T 的横截面细节。
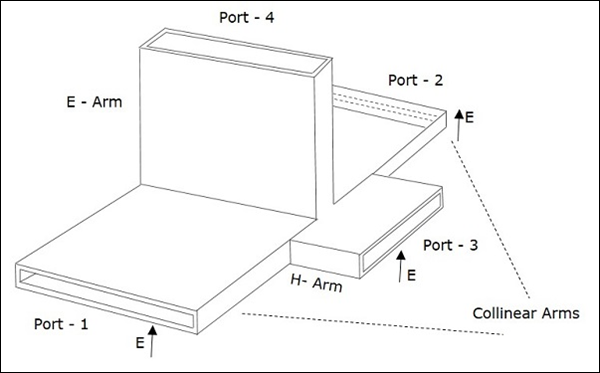
下图显示了侧臂与双向波导连接以形成并联和串联端口。
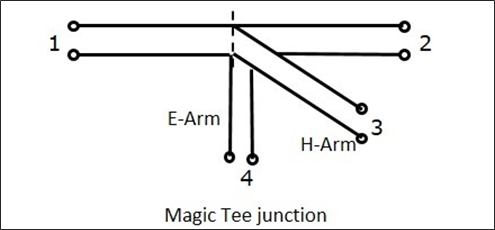
E-H 面 T 型接头的特性
如果将相位和幅度相等的信号发送到端口 1 和端口 2,则端口 4 的输出为零,而端口 3 的输出将是端口 1 和端口 2 的加和。
如果将信号发送到端口 4(E 臂),则功率在端口 1 和端口 2 之间平均分配,但相位相反,而端口 3 将没有输出。因此,$S_{34}$ = 0。
如果在端口 3 上馈入信号,则功率在端口 1 和端口 2 之间平均分配,而端口 4 将没有输出。因此,$S_{43}$ = 0。
如果在其中一个共线端口上馈入信号,则在另一个共线端口上不会出现输出,因为 E 臂产生相位延迟,而 H 臂产生相位提前。因此,$S_{12}$ = $S_{21}$ = 0。
E-H 面 T 型接头的属性
E-H 面 T 型接头的属性可以通过其$\left [ S \right ]_{4\times 4}$矩阵来定义。
它是一个 4×4 矩阵,因为有 4 个可能的输入和 4 个可能的输出。
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}& S_{14}\\ S_{21}& S_{22}& S_{23}& S_{24}\\ S_{31}& S_{32}& S_{33}& S_{34}\\ S_{41}& S_{42}& S_{43}& S_{44} \end{bmatrix}$ ........ 公式 1
由于它具有 H 面 T 型接头部分
$S_{23} = S_{13}$........ 公式 2
由于它具有 E 面 T 型接头部分
$S_{24} = -S_{14}$........ 公式 3
E 臂端口和 H 臂端口是如此隔离,以至于如果在一个端口上施加输入,则另一个端口不会产生输出。因此,这可以记为
$S_{34} = S_{43} = 0$........ 公式 4
根据对称性,我们有
$S_{ij} = S_{ji}$
$S_{12} = S_{21}, S_{13} = S_{31}, S_{14} = S_{41}$
$S_{23} = S_{32}, S_{24} = S_{42}, S_{34} = S_{43}$........ 公式 5
如果端口 3 和 4 与连接完美匹配,则
$S_{33} = S_{44} = 0$........ 公式 6
将上述所有公式代入公式 1 中,以获得 $[S]$ 矩阵,
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}& S_{14}\\ S_{12}& S_{22}& S_{13}& -S_{14}\\ S_{13}& S_{13}& 0& 0\\ S_{14}& -S_{14}& 0& 0 \end{bmatrix}$........ 公式 7
根据酉性,$[S][S]^\ast = [I]$
$\begin{bmatrix} S_{11}& S_{12}& S_{13}& S_{14}\\ S_{12}& S_{22}& S_{13}& -S_{14}\\ S_{13}& S_{13}& 0& 0\\ S_{14}& -S_{14}& 0& 0 \end{bmatrix} \begin{bmatrix} S_{11}^{*}& S_{12}^{*}& S_{13}^{*}& S_{14}^{*}\\ S_{12}^{*}& S_{22}^{*}& S_{13}^{*}& -S_{14}^{*}\\ S_{13}& S_{13}& 0& 0\\ S_{14}& -S_{14}& 0& 0 \end{bmatrix}$
$ = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
$R_1C_1 : \left | S_{11} \right |^2 + \left | S_{12} \right |^2 + \left | S_{13} \right |^2 = 1 + \left | S_{14} \right |^2 = 1$ ......... 公式 8
$R_2C_2 : \left | S_{12} \right |^2 + \left | S_{22} \right |^2 + \left | S_{13} \right |^2 = 1 + \left | S_{14} \right |^2 = 1$ ......... 公式 9
$R_3C_3 : \left | S_{13} \right |^2 + \left | S_{13} \right |^2 = 1$ ......... 公式 10
$R_4C_4 : \left | S_{14} \right |^2 + \left | S_{14} \right |^2 = 1$ ......... 公式 11
根据公式 10 和 11,我们得到
$S_{13} = \frac{1}{\sqrt{2}}$........ 公式 12
$S_{14} = \frac{1}{\sqrt{2}}$........ 公式 13
比较公式 8 和 9,我们有
$S_{11} = S_{22}$ ......... 公式 14
使用公式 12 和 13 中的这些值,我们得到
$\left | S_{11} \right |^2 + \left | S_{12} \right |^2 + \frac{1}{2} + \frac{1}{2} = 1$
$\left | S_{11} \right |^2 + \left | S_{12} \right |^2 = 0$
$S_{11} = S_{22} = 0$ ......... 公式 15
根据公式 9,我们得到 $S_{22} = 0$ ......... 公式 16
现在我们理解端口 1 和端口 2 与连接完美匹配。由于这是一个 4 端口连接,因此当两个端口完美匹配时,其他两个端口也与连接完美匹配。
所有四个端口都完美匹配的连接称为魔T 连接。
通过将公式 12 到 16 中的公式代入公式 7 中的 $[S]$ 矩阵,我们得到魔T 的散射矩阵为
$$[S] = \begin{bmatrix} 0& 0& \frac{1}{2}& \frac{1}{\sqrt{2}}\\ 0& 0& \frac{1}{2}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0& 0\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0& 0 \end{bmatrix}$$
我们已经知道,$[b]$ = $[S] [a]$
重写上述内容,我们得到
$$\begin{vmatrix} b_1\\ b_2\\ b_3\\ b_4 \end{vmatrix} = \begin{bmatrix} 0& 0& \frac{1}{2}& \frac{1}{\sqrt{2}}\\ 0& 0& \frac{1}{2}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0& 0\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}& 0& 0 \end{bmatrix} \begin{vmatrix} a_1\\ a_2\\ a_3\\ a_4 \end{vmatrix}$$
E-H 面 T 型接头的应用
E-H 面 T 型接头的一些最常见应用如下:
E-H 面连接用于测量阻抗 - 将零检测器连接到 E 臂端口,同时将微波源连接到 H 臂端口。共线端口与这些端口一起构成一个桥,阻抗测量通过平衡桥来完成。
E-H 面 T 型接头用作双工器 - 双工器是一个既充当发射器又充当接收器的电路,使用单个天线同时执行这两种功能。端口 1 和端口 2 用作接收器和发射器,它们彼此隔离,因此不会相互干扰。天线连接到 E 臂端口。匹配负载连接到 H 臂端口,不产生反射。现在,存在传输或接收而没有任何问题。
E-H 面 T 型接头用作混频器 - E 臂端口连接到天线,H 臂端口连接到本地振荡器。端口 2 具有匹配负载,没有反射,端口 1 具有混频器电路,该电路获得一半的信号功率和一半的振荡器功率以产生中频频率。
除了上述应用外,E-H 面 T 型接头还用作微波桥、微波鉴别器等。