
微波工程 - 微波器件
与其他系统一样,微波系统由许多微波组件构成,主要在一端具有电源,另一端具有负载,所有这些都通过波导、同轴电缆或传输线系统连接。
以下是波导的特性。
- 高信噪比
- 低衰减
- 较低的插入损耗
波导微波功能
考虑一个具有4个端口的波导。如果功率施加到一个端口,它会以一定的比例通过所有3个端口,其中一部分可能会从同一个端口反射回来。此概念在下图中清楚地描绘。
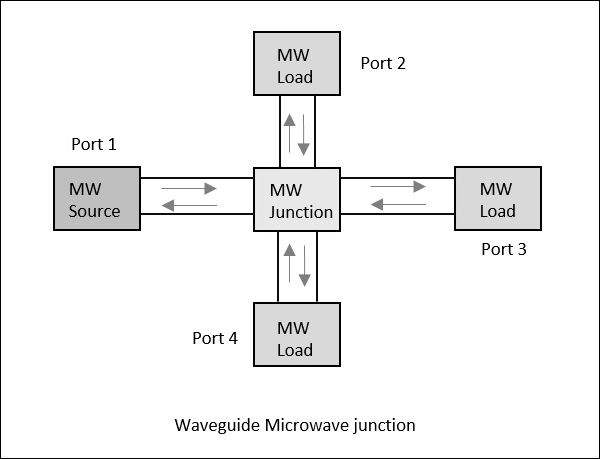
散射参数
对于一个二端口网络,如下图所示,如果功率施加在一个端口,正如我们刚才讨论的那样,大部分功率从另一个端口逸出,而一部分功率反射回同一个端口。在下图中,如果施加V1或V2,则分别流过I1或I2电流。
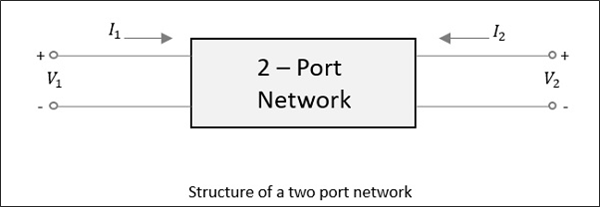
如果电源施加到相对的端口,则需要考虑另外两种组合。因此,对于一个二端口网络,可能出现2 × 2 = 4种组合。
当具有相关功率的行波通过端口散射时,微波结可以用S参数或散射参数来定义,这些参数以矩阵形式表示,称为“散射矩阵”。
散射矩阵
它是一个方阵,给出了微波结各种输入和输出端口之间所有功率关系的组合。该矩阵的元素称为“散射系数”或“散射(S)参数”。
考虑下图。
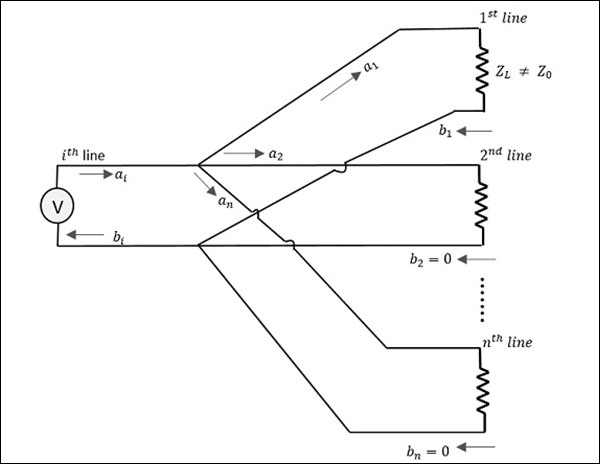
这里,电源通过第$i$条线连接,$a_1$是入射波,$b_1$是反射波。
如果给出一个$b_1$和$a_1$之间的关系,
$$b_1 = (反射系数)a_1 = S_{1i}a_1$$
其中
$S_{1i}$ = 第1条线的反射系数(其中$i$是输入端口,$1$是输出端口)
$1$ = 第1条线的反射
$i$ = 电源连接在第$i$条线上
如果阻抗匹配,则功率被传输到负载。如果负载阻抗与特性阻抗不匹配,则情况并非如此。然后,发生反射。这意味着如果
$$Z_l \neq Z_o$$
但是,如果这种不匹配存在于多个端口(例如'n'个端口),则i = 1到n(因为i可以是从1到n的任何线路)。
因此,我们有
$$b_1 = S_{11}a_1 + S_{12}a_2 + S_{13}a_3 + ............... + S_{1n}a_n$$
$$b_2 = S_{21}a_1 + S_{22}a_2 + S_{23}a_3 + ............... + S_{2n}a_n$$
$$.$$
$$.$$
$$.$$
$$.$$
$$.$$
$$b_n = S_{n1}a_1 + S_{n2}a_2 + S_{n3}a_3 + ............... + S_{nn}a_n$$
当整个内容以矩阵形式表示时,
$$\begin{bmatrix} b_1\\ b_2\\ b_3\\ .\\ .\\ .\\ b_n \end{bmatrix} = \begin{bmatrix} S_{11}& S_{12}& S_{13}& ...& S_{1n}\\ S_{21}& S_{22}& S_{23}& ...& S_{2n}\\ .& .& .& ...& . \\ .& .& .& ...& . \\ .& .& .& ...& . \\ S_{n1}& S_{n2}& S_{n3}& ...& S_{nn}\\ \end{bmatrix} \times \begin{bmatrix} a_1\\ a_2\\ a_3\\ .\\ .\\ .\\ a_n \end{bmatrix}$$
列矩阵 $[b]$ 散射矩阵 $[S]$矩阵 $[a]$
列矩阵$\left [ b \right ]$对应于反射波或输出,而矩阵$\left [ a \right ]$对应于入射波或输入。n×n阶的散射列矩阵$\left [ s \right ]$包含反射系数和传输系数。因此,
$$\left [ b \right ] = \left [ S \right ]\left [ a \right ]$$
[S]矩阵的性质
散射矩阵表示为[S]矩阵。[S]矩阵有一些标准性质。它们是:
-
[S]始终是(nxn)阶的方阵
[S]n×n
-
[S]是对称矩阵
即,$S_{ij} = S_{ji}$
-
[S]是酉矩阵
即,$[S][S]^* = I$
任何一行或一列的每一项乘以另一行或一列的对应项的复共轭的乘积之和为零。即,
$$\sum_{i=j}^{n} S_{ik} S_{ik}^{*} = 0 \: for \: k \neq j$$
$$( k = 1,2,3, ... \: n ) \: and \: (j = 1,2,3, ... \: n)$$
-
如果某个第k个端口与结之间的电距离为$\beta _kI_k$,则涉及k的$S_{ij}$系数将乘以因子$e^{-j\beta kIk}$
在接下来的几章中,我们将研究不同类型的微波三通。