微波工程 - 传输线
传输线是一种连接器，用于将能量从一点传输到另一点。传输线理论的研究有助于有效地利用电力和设备。
基本上有四种类型的传输线：
- 双线平行传输线
- 同轴线
- 带状基板传输线
- 波导
在传输或接收过程中，能量传输必须有效地进行，而不会浪费电力。为了实现这一点，必须考虑某些重要参数。
传输线的主要参数
传输线的重要参数包括电阻、电感、电容和电导。
电阻和电感一起称为传输线阻抗。
电容和电导一起称为导纳。
电阻
传输线制作材料的电阻将相当大，特别是对于较短的线路。随着线路电流的增加，欧姆损耗 I²R 损耗 也增加。
长度为“l”、横截面积为“a”的导体的电阻R表示为
R = \rho \frac{l}{a}
其中
ρ = 导体材料的电阻率，为常数。
温度和电流频率是影响线路电阻的主要因素。导体的电阻随温度变化线性变化。而如果电流频率增加，导体表面的电流密度也增加。否则，导体中心的电流密度增加。
这意味着，电流越向导体表面流动，向中心流动的电流就越少，这被称为趋肤效应。
电感
在交流传输线中，电流呈正弦波变化。此电流感应出垂直于电场的磁场，该磁场也呈正弦波变化。这被称为法拉第定律。下图显示了这些场。
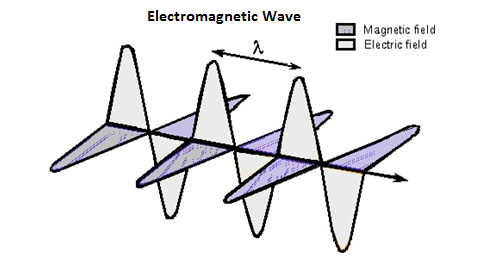
这个变化的磁场在导体中感应出一些电动势。现在，这个感应电压或电动势沿与最初流动的电流相反的方向流动。这个沿相反方向流动的电动势等效地由一个称为电感的参数表示，它是阻碍电流变化的特性。
用“L”表示。测量单位为“亨利H”。
电导
传输线与地之间以及相导线之间将存在漏电流。少量漏电流通常通过绝缘体的表面流动。此漏电流的倒数称为电导。用“G”表示。
线路电流的流动与电感有关，两点之间的电压差与电容有关。电感与磁场有关，而电容与电场有关。
电容
相导线之间的电压差导致导线之间产生电场。两条导线就像平行板，它们之间的空气成为电介质。这种模式导致导线之间产生电容效应。
特性阻抗
如果考虑均匀无损传输线，对于沿一个方向传播的波，沿该线电压和电流幅度的比率（没有反射）称为特性阻抗。
用 Z₀ 表示
Z_0 = \sqrt{\frac{电压波值}{电流波值}}
Z_0 = \sqrt{\frac{R + jwL}{G + jwC}}
对于无损线路，R₀ = √L/C
其中 L & C 分别是单位长度的电感和电容。
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
阻抗匹配
为了将最大功率传输到负载，必须进行阻抗匹配。为了实现这种阻抗匹配，必须满足以下条件：
负载电阻应等于电源电阻。
R_L = R_S
负载电抗应等于电源电抗，但符号相反。
X_L = -X_S
这意味着，如果电源是电感性的，则负载应是电容性的，反之亦然。
反射系数
表示由于传输线阻抗不匹配而产生的反射能量的参数称为反射系数。用 ρ rho 表示。
它可以定义为“负载端子处反射电压与入射电压之比”。
\rho = \frac{反射电压}{入射电压} = \frac{V_r}{V_i} \: 在 \: 负载 \: 端子 \: 处
如果器件和传输线之间的阻抗不匹配，则能量会反射。反射能量越高，ρ 反射系数的值越大。
电压驻波比 VSWR
当入射波反射时，会形成驻波。形成的驻波包含一些电压。驻波的幅度可以用驻波比来衡量。
驻波中最大电压与最小电压之比可以定义为电压驻波比 VSWR。用“S”表示。
S = \frac{\left |V_{max} \right |}{\left |V_{min} \right |} \quad 1\:\leq S \leq \infty
VSWR 描述了由于入射波和反射波的相加和相减而在传输线中存在的电压驻波模式。
因此，它也可以写成
S = \frac{1 + \rho }{1 - \rho }
阻抗失配越大，驻波的幅度就越高。因此，如果阻抗完全匹配，
V_{max} : V_{min} = 1:1
因此，VSWR 的值为 1，这意味着传输是完美的。
传输线的效率
传输线的效率定义为输出功率与输入功率之比。
传输线效率 % η = 接收端接收到的功率 / 从传输端发送的功率 × 100
电压调整率
电压调整率定义为传输线发送端和接收端电压幅度的变化。
电压调整率 % = 发送端电压 - 接收端电压 / 发送端电压 × 100
由于阻抗不匹配造成的损耗
如果传输线没有以匹配负载端接，则会发生损耗。这些损耗有多种类型，例如衰减损耗、反射损耗、传输损耗、回波损耗、插入损耗等。
衰减损耗
由于信号在传输线中的吸收而发生的损耗称为衰减损耗，表示为
衰减损耗 (dB) = 10 \: log_{10} \left [ \frac{E_i - E_r}{E_t} \right ]
其中
Eᵢ = 输入能量
Eᵣ = 从负载反射到输入的能量
Eₜ = 传输到负载的能量
反射损耗
由于传输线阻抗不匹配而导致信号反射而发生的损耗称为反射损耗，表示为
反射损耗 (dB) = 10 \: log_{10} \left [ \frac{E_i}{E_i - E_r} \right ]
其中
Eᵢ = 输入能量
Eᵣ = 从负载反射的能量
传输损耗
在传输线传输过程中发生的损耗称为传输损耗，表示为
传输损耗(dB) = 10 \: log_{10} \: \frac{E_i}{E_t}
其中
Eᵢ = 输入能量
Eₜ = 传输的能量
回波损耗
传输线反射功率的度量称为回波损耗，表示为
回波损耗(dB) = 10 \: log_{10} \: \frac{E_i}{E_r}
其中
Eᵢ = 输入能量
Eᵣ = 反射能量
插入损耗
使用传输线进行能量传输与不使用传输线进行能量传输相比发生的损耗称为插入损耗，表示为
插入损耗(dB) = 10 \: log_{10} \: \frac{E_1}{E_2}
其中
E₁ = 负载直接连接到电源时（无传输线）接收到的能量。
E₂ = 负载和电源之间连接传输线时负载接收到的能量。
阻抗匹配
如果负载阻抗与源阻抗不匹配，则有时使用称为“阻抗匹配”的方法来实现匹配。
在某一点或多点处与主线并联连接开路或短路线段（称为阻抗匹配）的过程，可以称为阻抗匹配。
在较高的微波频率下，主要采用两种阻抗匹配技术。
单端匹配
在单端匹配中，将一定固定长度的短截线放置在距负载一定距离处。它仅用于固定频率，因为对于任何频率变化，都必须改变短截线的位置，而这通常不会进行。此方法不适用于同轴线。
双端匹配
在双端匹配中，两个可变长度的短截线固定在某些位置。当负载变化时，只需调整短截线的长度即可实现匹配。这在实验室实践中被广泛用作单频匹配设备。
下图显示了阻抗匹配的外观。
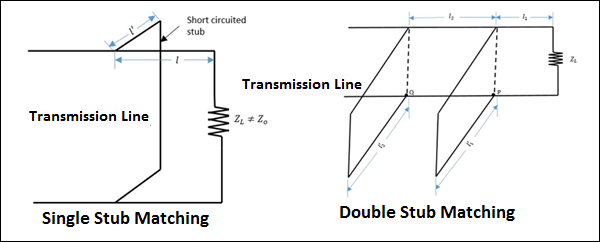
如上图所示，在传输线中进行单端匹配和双端匹配以实现阻抗匹配。