一个木块以$10 \mathrm{~m} / \mathrm{s}$的速度运动，并受到一个大小为$100N$的力，此外摩擦力也作用在木块上。求木块的加速度。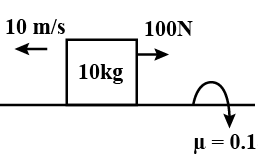"\n

已知

质量，$m$ = 10 kg

速度，$v$ = 10 m/s

力，$F$ = 100 N

求解：木块的加速度，或木块的负加速度$(a_r)$。

解答

我们知道摩擦力表示为-

$f=\mu N$

$f$ = 摩擦力

$\mu$ = 摩擦系数

$N$ = 垂直压力

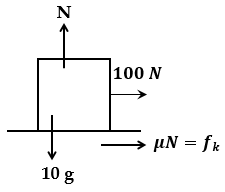
由于存在相对运动

因此动摩擦力将减小这种相对运动。

$f_k=\mu N$

$f_k=\mu mg$     $(\because N=mg)$

将给定值代入上式，得到-

$f_k=0.1\times {10}\times {10}=10N$

因此，木块上的合力将为-

$100N+10N=110N$

现在，我们知道加速度，$a$ 表示为-

$a=\frac {F}{m}$

因此，这里-

$a_r=\frac {F_{net}}{m}$

$a_r=\frac {110}{10}$

$a=11m/s^2$

因此，木块的加速度，或木块的负加速度$(a_r)$为11m/s².

Tutorialspoint

更新于: 2022年10月10日

46 次浏览

开启你的职业生涯

通过完成课程获得认证

立即开始