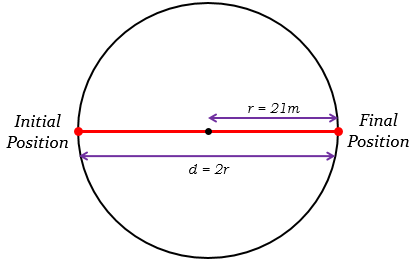
一个质量为\( 40 \mathrm{~kg} \)的男孩在一个半径为\( 21 \mathrm{~m} \)的圆形跑道上运动。求当他的初始位置和最终位置位于直径的两端时，他的位移和路程。

已知

圆形跑道的半径，$r$ = 21 m

求解：位移和路程。

解答

由于初始位置和最终位置位于直径的两端，这意味着男孩跑完了半圈（半圆）。

为了求路程，我们需要求半圆的周长。

我们知道：

$周长，(C)=2\pi {r}$

因此半圆的周长$=\frac {2\pi {r}}{2}=\pi {r}$

因此，

男孩跑半圈的路程$=\frac {22}{7}\times {21}=22\times {3}=66m$

位移 = 初始位置和最终位置之间的最短距离 = 圆的直径 $=2\times {r}=2\times {21}=42m$

教程点

更新于： 2022年10月10日

63 次浏览

开启你的职业生涯

完成课程获得认证

开始学习