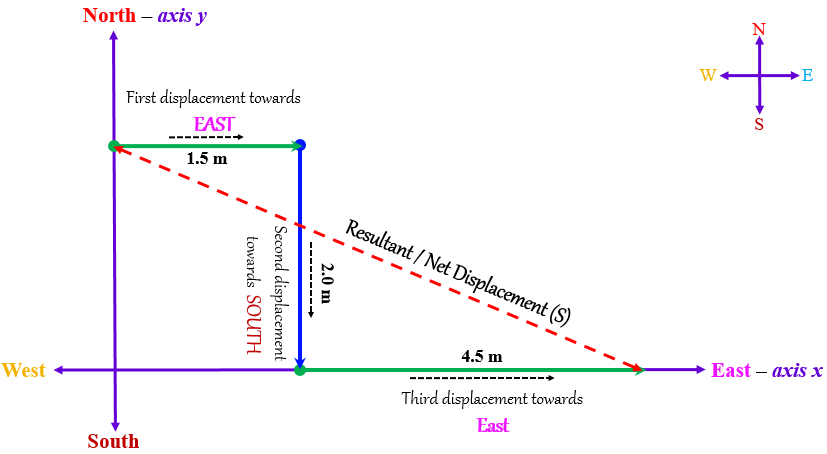
一人向东走 1.5 米，然后向南走 2.0 米，再向东走 4.5 米。求此人总共走过的距离？求其最终位移？

距离指的是物体总共走过的路程（它只有大小，没有方向）。

因此，此人总共走过的距离为 = 1.5 + 2.0 + 4.5 = 8 米。

位移只不过是位置的变化（它既有大小也有方向）。它是从起始位置到最终位置的最短距离。

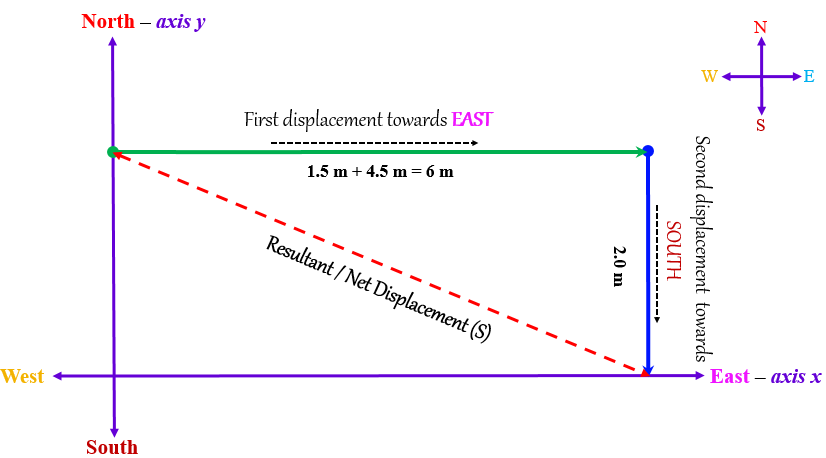
根据题意，此人向东方向走了1.5 米和4.5 米，向南方向只走了2.0 米。因此，我们可以直接画一个向东 6 米和向南 2 米的图，其结果相同。

这里，我们使用当距离单位用于指定初始和最终位置时的合位移公式。

合位移公式写为：$S=\sqrt{{x}^{2}+{y}^{2}}$。

其中 'S' 代表位移。X 是物体运动的第一个方向（向东 6 米），Y 是物体运动的第二个方向（向南 2 米）。

现在，将值代入公式中，我们得到：

$S=\sqrt{{6}^{2}+{2}^{2}}$

$S=\sqrt{36+4}$

$S=\sqrt{40}$

$S=2\sqrt{10}$

因此，合位移将为$2\sqrt{10}$。

Tutorialspoint

更新于：2022年10月10日

4K+ 次浏览

开启你的职业生涯

完成课程获得认证

开始学习